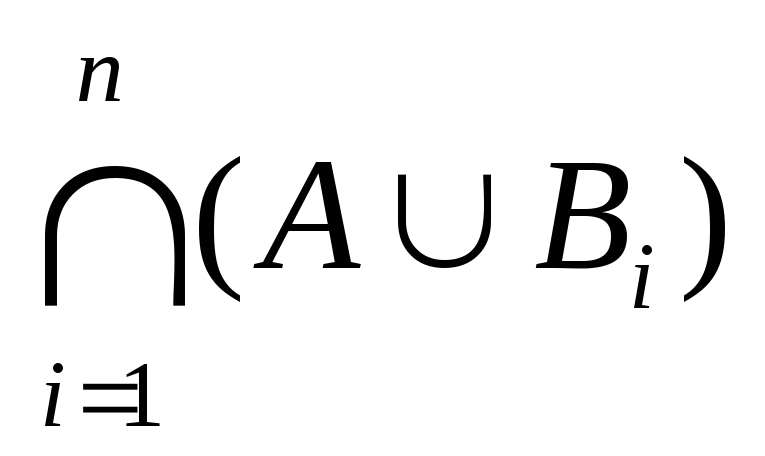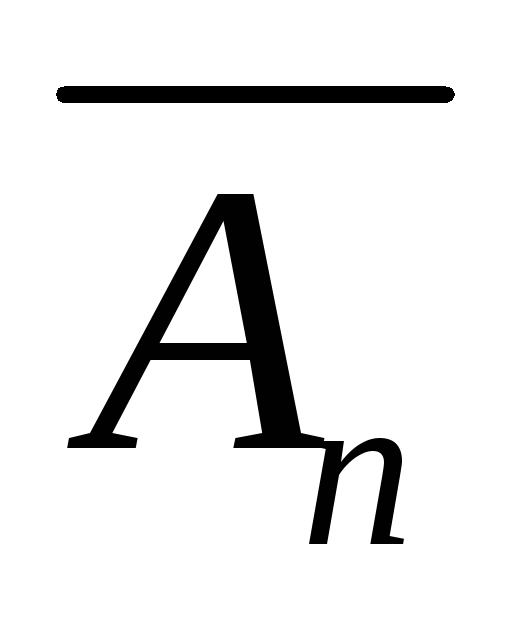ЛЕКЦИЯ №3 Доказательство тождеств
Цель: 1. Повторить определения тождества и тождественно равных выражений.
2.Ввести понятие тождественного преобразования выражений.
3. Умножение многочлена на многочлен.
4. Разложение многочлена на множители способом группировки.
Пусть каждый день и каждый час
Пусть добрым будет ум у нас,
В математике существует множество понятий. Одно из них тождество.
Тождеством называют равенство, которое выполняется при всех значениях переменных, которые в него входят. Некоторые тождества мы уже знаем.
Например, все формулы сокращенного умножения являются тождествами.
Формулы сокращенного умножения
4. a3 ± b3 = (a ± b)(a2 
Доказать тождество – это значит установить, что для любого допустимого значение переменные его левая часть равна правой части.
В алгебре существует несколько различных способов доказательства тождеств.
Способы доказательства тождеств
- Выполнить равносильные преобразования левой части тождества. Если в итоге получим правую часть, тогда тождество считается доказанным. Выполнить равносильные преобразования правой части тождества. Если в итоге получим левую часть, тогда тождество считается доказанным. Выполнить равносильные преобразования левой и правой части тождества. Если в результате получим одинаковый результат, тогда тождество считается доказанным. Из правой части тождества вычитаем левую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным. Из левой части тождества вычитают правую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным.
Следует так же помнить, что тождество справедливо лишь для допустимых значений переменных.
Как видите способов достаточно много. Какой способ выбрать в данном конкретном случае, зависит от тождества, которое вам необходимо доказать. По мере того, как вы будете доказывать различные тождества, придет и опыт в выборе способа доказательства.
Тождество — это уравнение, которое удовлетворяется тождественно, т. е. справедливо для любых допустимых значений входящих в него переменных. Доказать тождество — значит установить, что при всех допустимых значениях переменных его левая и правая части равны.
Способы доказывания тождества:
1. Выполняют преобразования левой части и получают в итоге правую часть.
2. Выполняют преобразования правой части и в итоге получают левую часть.
3. По отдельности преобразуют правую и левую части и получают и в первом и во втором случае одно и то же выражение.
4. Составляют разность левой и правой части и в результате её преобразований получают нуль.
Рассмотрим несколько простых примеров
Пример 1. Докажите тождество x·(a+b) + a·(b-x) = b·(a+x).
Так как в правой части небольшое выражение, попытаемся преобразовать левую часть равенства.
Приведем подобные слагаемые и вынесем общий множитель за скобку.
x·a + x·b + a·b – a·x = x·b + a·b = b·(a + x).
Получили что левая часть после преобразований, стала такой же как и правая часть. Следовательно, данное равенство является тождеством.
В данном примере можно поступить следующим способом. Раскроем скобки в правой части равенства.
(a+5)·(a+2) = (a²) + 5·a +2·a +10 = a²+7·a + 10.
Видим, что после преобразований, правая часть равенства стала такой же как и левая часть равенства. Следовательно, данное равенство является тождеством.
« Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения»
Выяснить какое равенство является тождеством:
4. рху ( — р2 х2 у) = — р3 х3 у3.
«Чтобы доказать, что некоторое равенство является тождеством, или, как говорят иначе, чтобы доказать тождество, используют тождественные преобразования выражений»
Равенство верное при любых значениях переменных, называют тождеством. Чтобы доказать, что некоторое равенство является тождеством, или, как говорят иначе, чтобы доказать тождество, используют тождественные преобразования выражений.
Докажем тождество:
xy — 3y — 5x + 16 = (x — 3)(y — 5) + 1 Преобразуем левую часть этого равенства:
xy — 3y — 5x + 16 = (xy — 3y) + (- 5x + 15) +1 = y(x — 3) — 5(x -3) +1 = (y — 5)(x — 3) +1 В результате тождественного преобразования левой части многочлена мы получили его правую часть и тем самым доказали, что данное равенство является тождеством.
Для доказательства тождества преобразуют его левую часть в правую или его правую часть в левую, или показывают, что левая и правая части исходного равенства тождественно равны одному и тому же выражению.
Умножение многочлена на многочлен
Умножим многочлен a + b на многочлен c + d. Составим произведение этих многочленов:
(a+b)(c+d).
Обозначим двучлен a + b буквой x и преобразуем полученное произведение по правилу умножения одночлена на многочлен:
(a+b)(c+d) = x(c+d) = xc + xd.
В выражение xc + xd. подставим вместо x многочлен a+b и снова воспользуемся правилом умножения одночлена на многочлен:
xc + xd = (a+b)c + (a+b)d = ac + bc + ad + bd.
Итак: (a+b)(c+d) = ac + bc + ad + bd.
Произведение многочленов a + b и c + d мы представили в виде многочлена ac + bc + ad + bd. Этот многочлен является суммой всех одночленов, получающихся при умножении каждого члена многочлена a + b на каждый член многочлена c + d.
Вывод: произведение любых двух многочленов можно представить в виде многочлена.
Правило: чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.
Заметим, что при умножении многочлена, содержащего m членов на многочлен, содержащий n членов в произведении до приведения подобных членов должно получиться mn членов. Этим можно воспользоваться для контроля.
Разложение многочлена на множители способом группировки:
Ранее мы познакомились с разложением многочлена на множители путем вынесения общего множителя за скобки. Иногда удается разложить многочлен на множители, используя другой способ — группировку его членов.
Разложим на множители многочлен
ab — 2b + 3a — 6 Сгруппируем его так, чтобы слагаемые в каждой группе имели общий множитель и вынесем этот множитель за скобки:
ab — 2b + 3a — 6 = (ab — 2b) + (3a — 6) = b(a — 2) + 3(a — 2) Каждое слагаемое получившегося выражения имеет общий множитель (a — 2). Вынесем этот общий множитель за скобки:
b(a — 2) + 3(a — 2) = (b +3)(a — 2) В итоге мы разложили исходный многочлен на множители:
ab — 2b + 3a — 6 = (b +3)(a — 2) Способ, который мы применили для разложения многочлена на множители называют способом группировки.
Разложение многочлена ab — 2b + 3a — 6 на множители можно выполнить, группируя его члены иначе:
ab — 2b + 3a — 6 = (ab + 3a) + (- 2b — 6) = a(b + 3) -2(b + 3) = (a — 2)(b + 3)
1. Способы доказательства тождеств.
2. Что называют тождественным преобразованием выражения.
3. Умножение многочлена на многочлен.
4. Разложение многочлена на множители способом группировки
источник
! 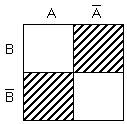
A \ B = A \ B = A 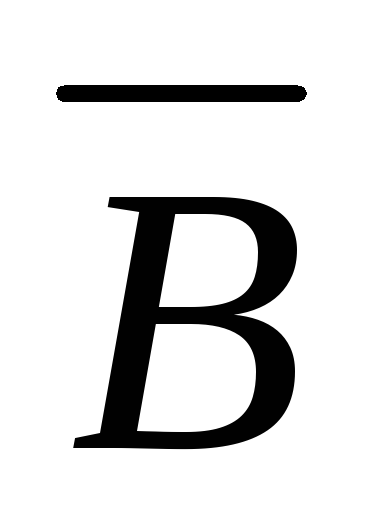
B \ A = B \ A = B 
Замечание. Отношения включения множеств могут быть определены в терминах и .
Следующие утверждения о произвольных множествах А и В попарно эквивалентны:
А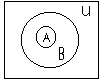
С помощью законов алгебры множеств можно упрощать выражения, содержащие множества.
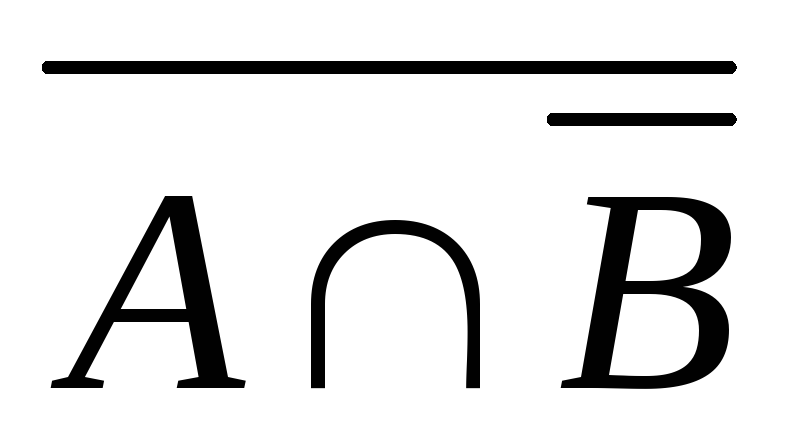





(A \ B) (A B) = (A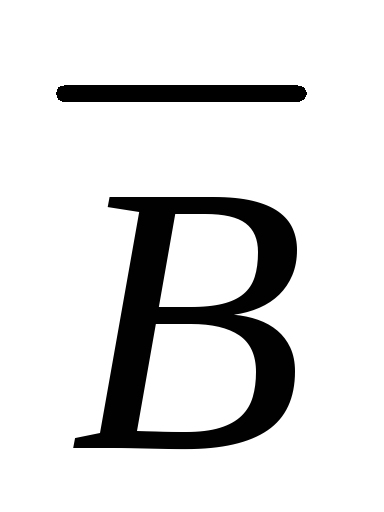
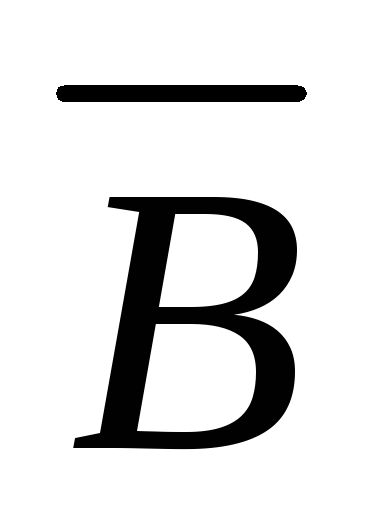
а) A (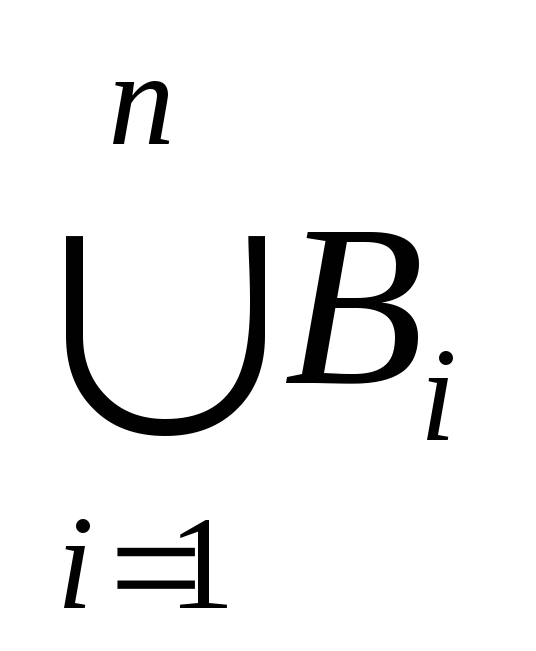
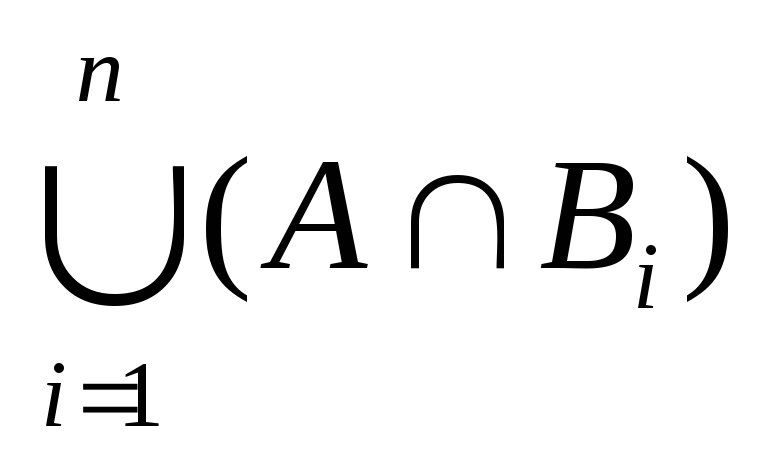
б) A (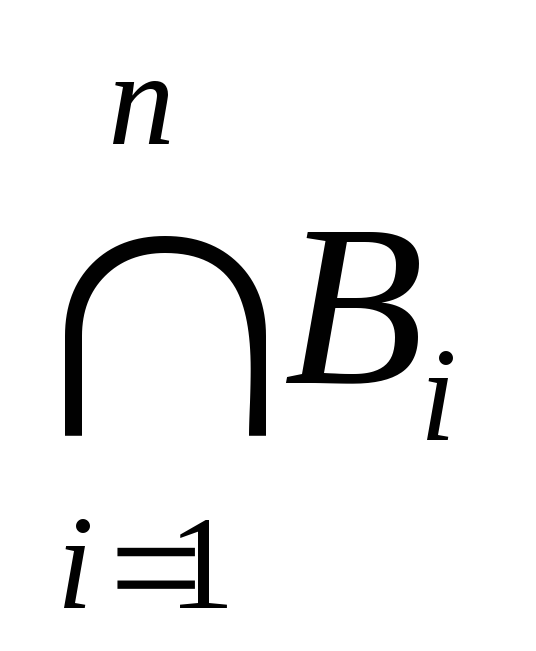
Доказательство утверждения (а) (методом математической индукции):
правая часть (1) = (AB1)(AB2) левая часть=правая часть (по доказанному ранее закону дистрибутивности пересечения относительно объединения).
2) Допустим, формула (а) верна при каком-то произвольном натуральном n=k (k2), т.е. допустим, что справедливо равенство: A(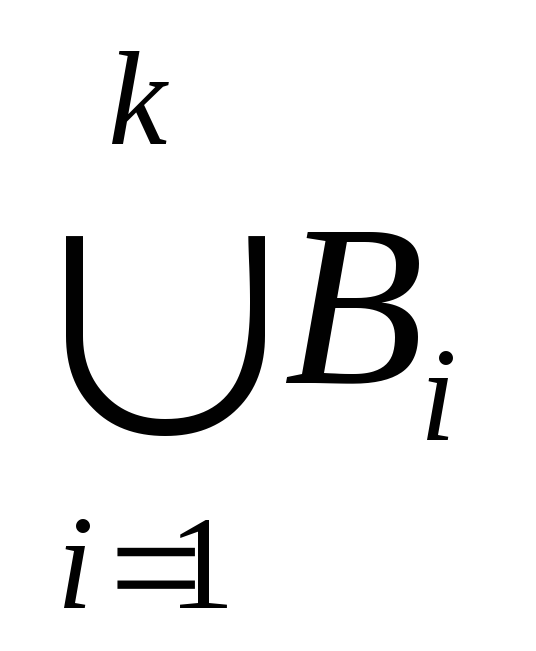
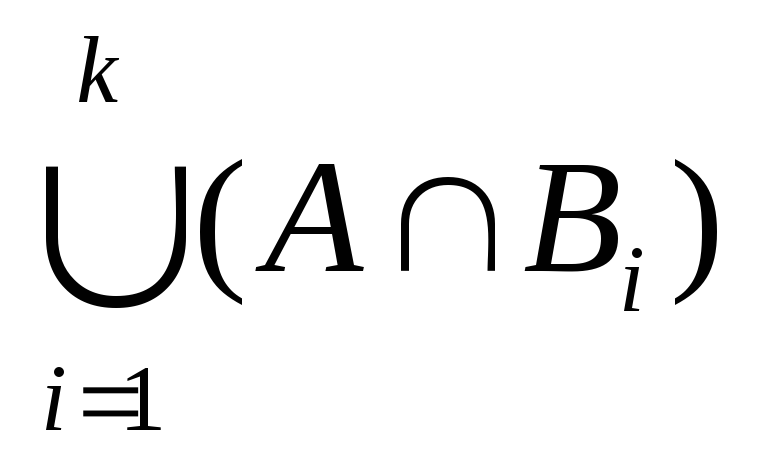
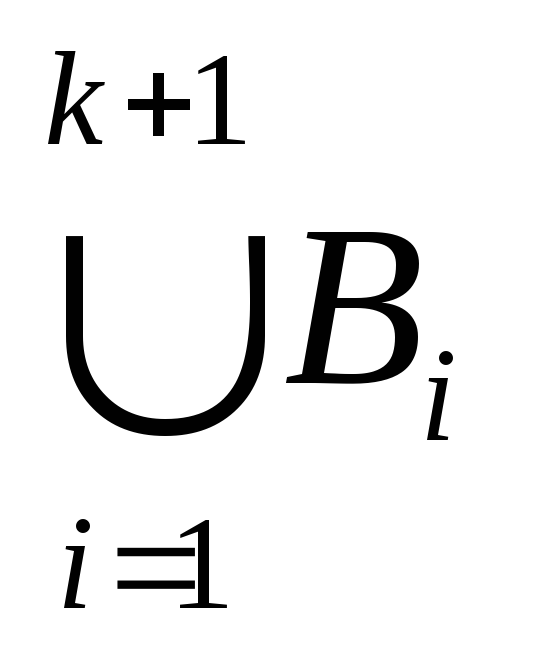
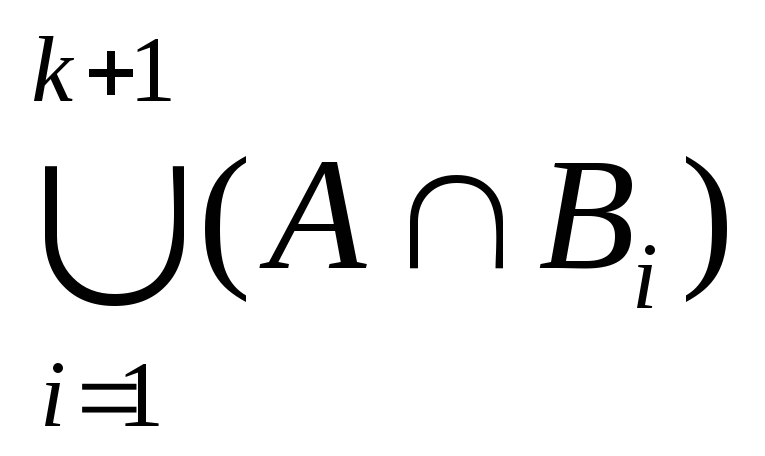
Доказательство: A (
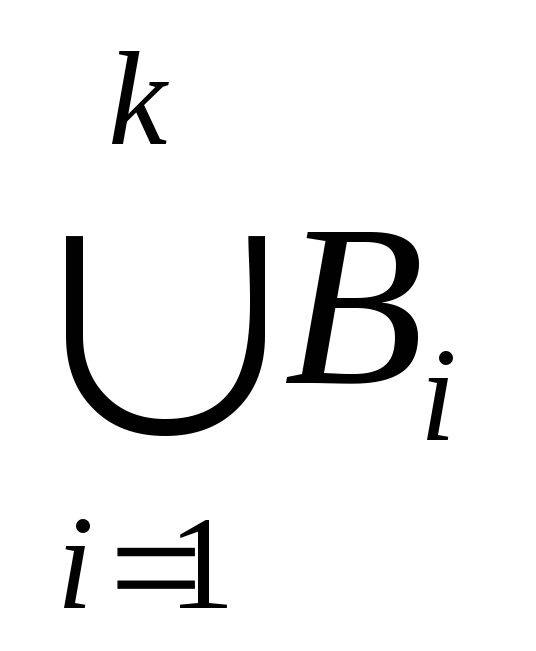
= (A (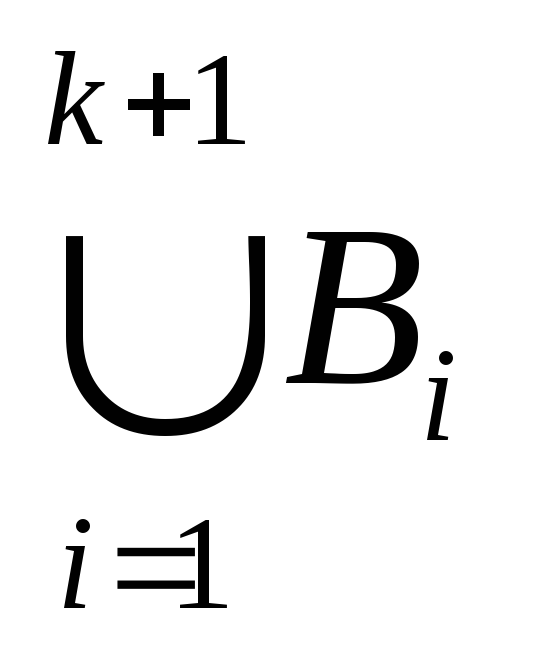
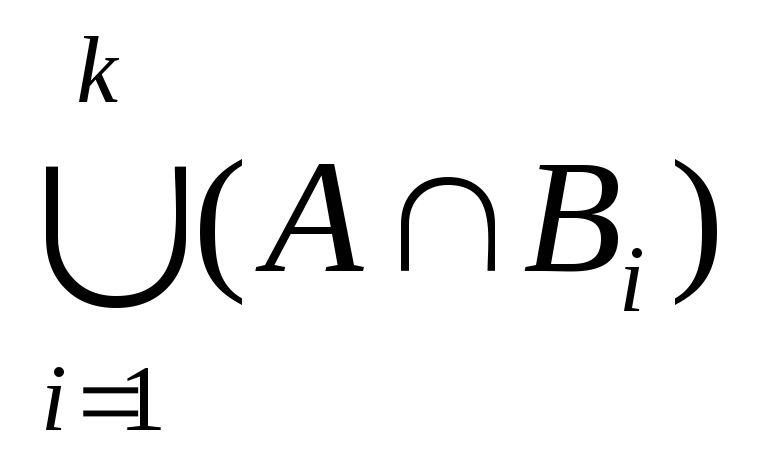
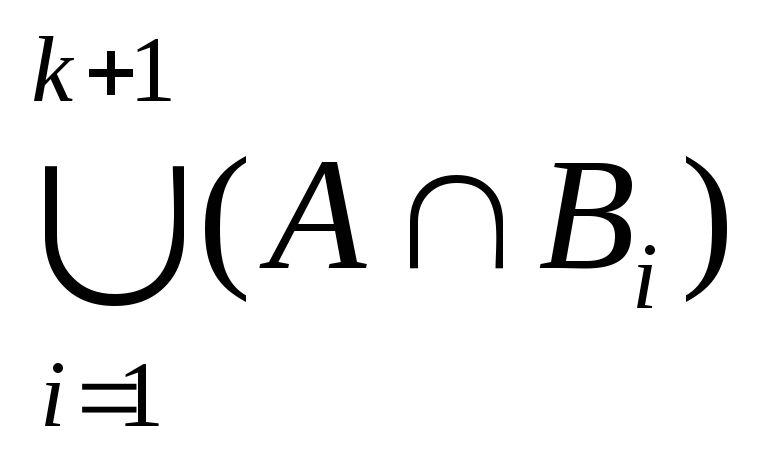
Так как утверждение (а) верно при n=2 и из истинности его при каком-то произвольном натуральном n=k (k 2) следует его справедливость и при следующем n=k+1, то равенство (1) верно для всех натуральных n2 на основании обобщенного принципа математической индукции.
Обобщенный закон де Моргана
а) 
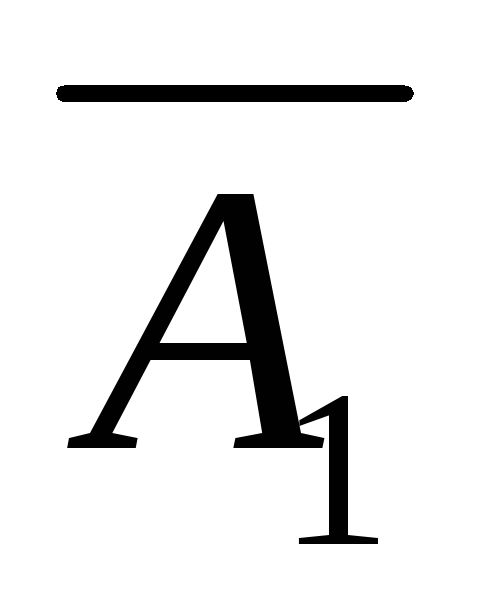

б) 
Доказательство утверждения (а) (методом математической индукции):
1) n = 2: левая часть = 
правая часть = 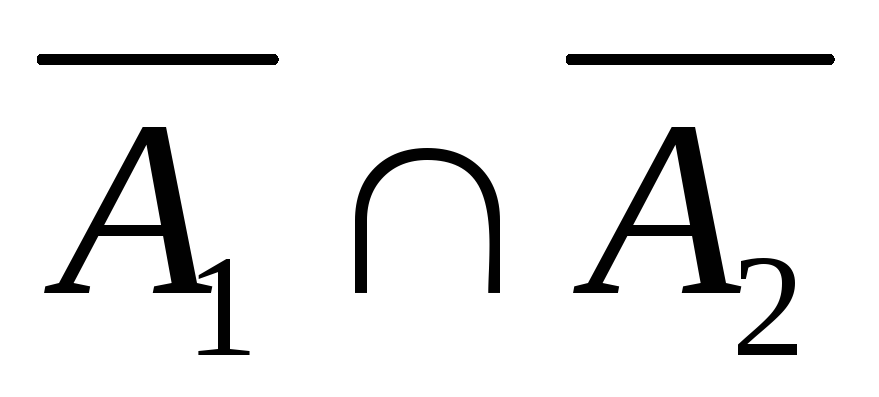
2) Допустим: 

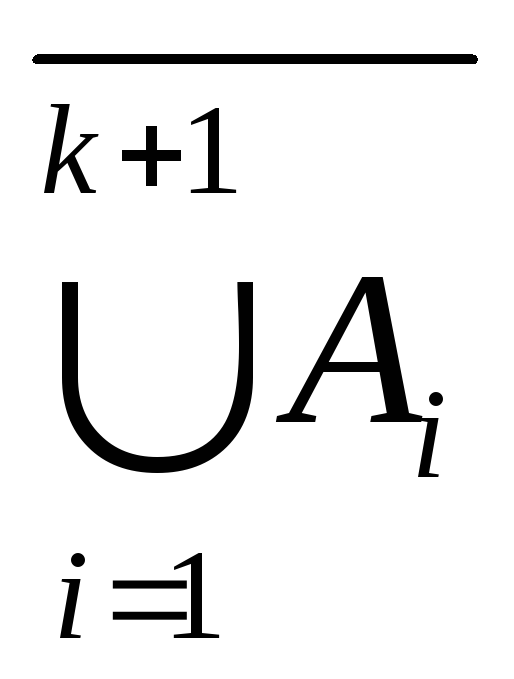
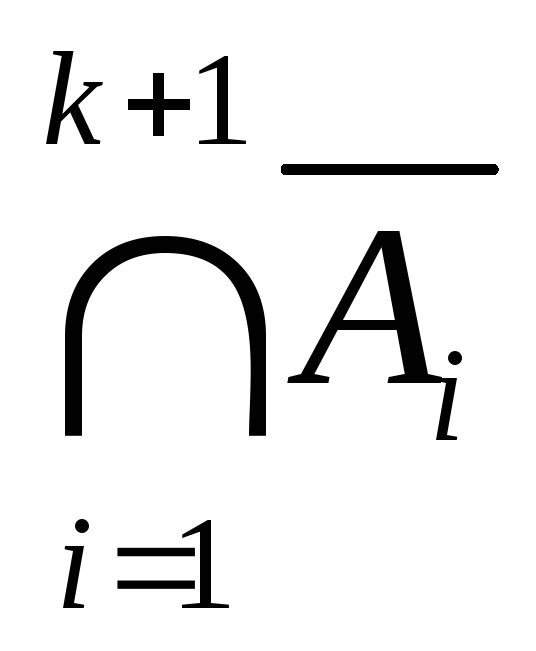
Доказательство: 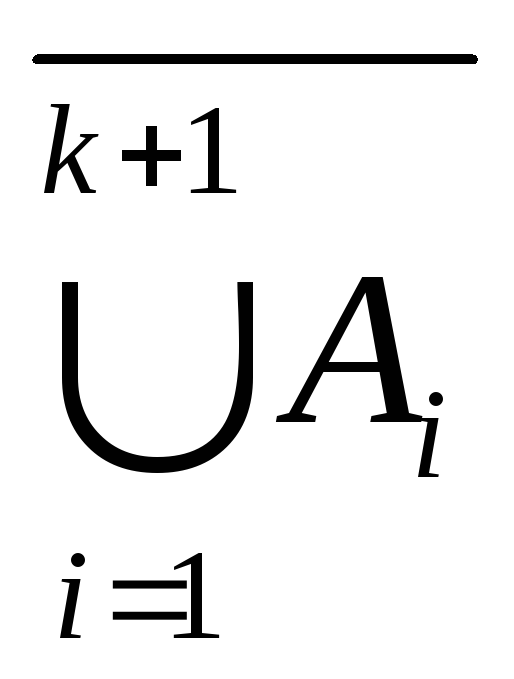
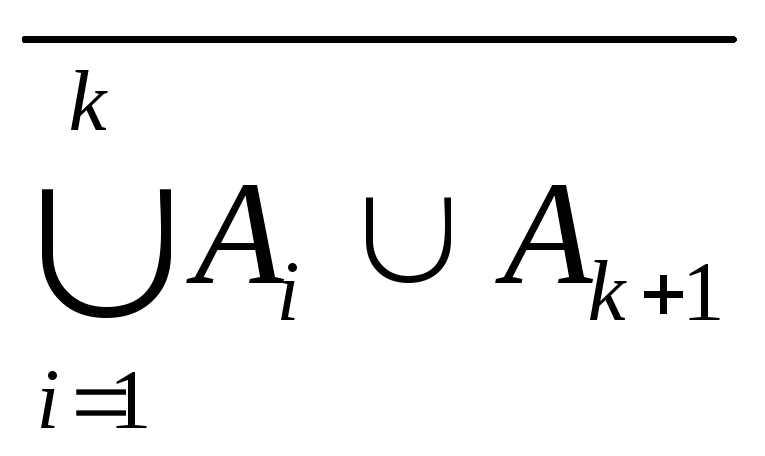
= 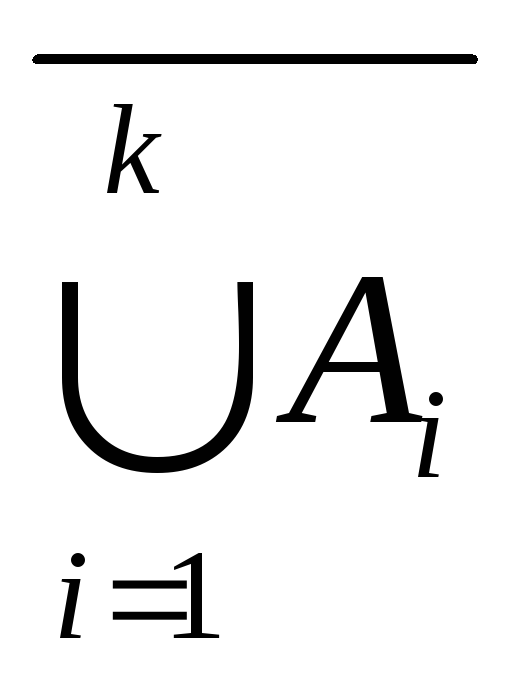
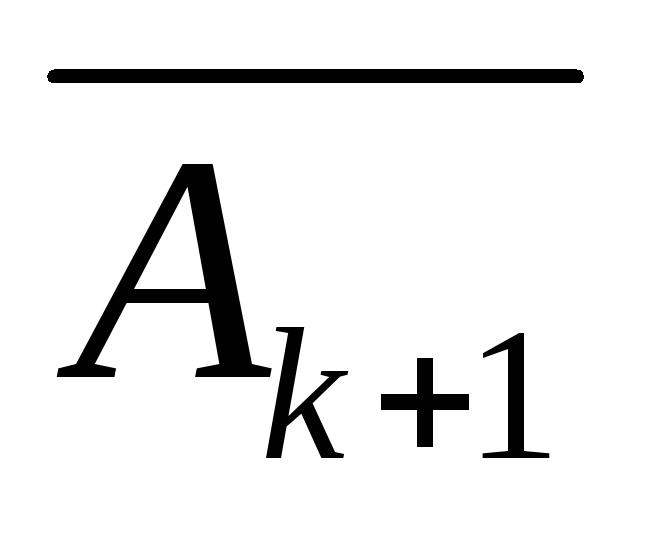



Так как выполнены оба условия обобщенного принципа математической индукции, то равенство (1) верно для всех натуральных n2.
Мощность множества – это количество элементов множества.
В множествах A’, B’, C’ n элементов, т.е. | A’| = |B’| = |C’| = n
Определение 1.15. Между множествами А и В установлено взаимно-однозначное соответствие, если элементы этих множеств объединены в пары и каждый элемент попал в одну и только одну пару.
Определение 1.16. Два множества (конечных или бесконечных) имеют одинаковую мощность, если между этими множествами можно установить взаимно-однозначное соответствие.
Определение 1.17. Множество бесконечно тогда и только тогда, когда оно имеет одинаковую мощность с некоторым своим подмножеством, не совпадающим с самим этим множеством.
П
Определение 1.18. Множество Х называется счетным, если его мощность равна мощности множества натуральных чисел, т.е. |X| = |N|.
Пример: Натуральные и целые числа равны по мощности! Равенство |N| = |Z| докажем установлением следующего соответствия: n
Утверждения о счетности множеств:
Любое подмножество счетного множества не более чем счетно.
Объединение счетного множества конечных множеств счетно.
Объединение счетного или конечного числа счетных множеств счетно.
Определение 1.19. Мощность множества А меньше мощности множества В (|A| |N|.
Доказательство: От противного. Допустим, отрезок [0; 1] – счетное множество. Значит, существует его нумерация. Расположим все числа, изображенные бесконечными десятичными дробями в порядке этой нумерации:
Рассмотрим любую бесконечную десятичную дробь 0, b1b2b3 … такую, что b1a11, b2a22, b3a33 и т.д. Эта дробь не может войти в указанную последовательность, т.к. от 1-го числа она отличается 1-ой цифрой после запятой, от 2-го – 2-ой цифрой и т.д. Следовательно, все числа из [0; 1] не могут быть пронумерованы. Значит, предположение от счетности отрезка [0; 1] неверно.
Замечание. Используемый в доказательстве метод рассуждений получил название диагонального метода Кантора.
Определение 1.20. Мощность отрезка [0; 1] называется континуумом. Множество такой мощности называется континуальным.
источник
Найдем значения выражений 2(х — 1) 2х — 2 для данных значений переменной х. Результаты запишем в таблицу:
Можно прийти к выводу, что значения выражений 2(х — 1) 2х — 2 для каждого данного значения переменной х равны между собой. По распределительным свойством умножения относительно вычитания 2(х — 1) = 2х — 2. Поэтому и для любого другого значения переменной х значение выражения 2(х — 1) 2х — 2 тоже будут равны между собой. Такие выражения называют тождественно равными.
Например, синонимами являются выражения 2х + 3х и 5х, так как при каждом значении переменной х эти выражения приобретают одинаковых значений (это вытекает из распределительной свойства умножения относительно сложения, поскольку 2х + 3х = 5х).
Рассмотрим теперь выражения 3х + 2у и 5ху. Если х = 1 и в = 1, то соответствующие значения этих выражений равны между собой:
3х + 2у =3 ∙ 1 + 2 ∙ 1 =5; 5ху = 5 ∙ 1 ∙ 1 = 5.
Однако можно указать такие значения х и у, для которых значения этих выражений не будут между собой равными. Например, если х = 2; у = 0, то
3х + 2у = 3 ∙ 2 + 2 ∙ 0 = 6, 5ху = 5 ∙ 20 = 0.
Следовательно, существуют такие значения переменных, при которых соответствующие значения выражений 3х + 2у и 5ху не равны друг другу. Поэтому выражения 3х + 2у и 5ху не являются тождественно равными.
Исходя из вышеизложенного, тождественностями, в частности, являются равенства: 2(х — 1) = 2х — 2 и 2х + 3х = 5х.
Тождеством является каждое равенство, которым записано известные свойства действий над числами. Например,
а + b = b + а; (а + b) + с = а + (b + с); а(b + с) = ab + ас;
ab = bа; (аb)с = a(bc); a(b — с) = ab — ас.
Тождественностями есть и такие равенства:
Тождественностями также принято считать верные числовые равенства, например:
1 + 2 + 3 = 6; 5 2 + 12 2 = 13 2 ; 12 ∙ (7 — 6) = 3 ∙ 4.
Если в выражении-5х + 2х — 9 свести подобные слагаемые, получим, что 5х + 2х — 9 = 7х — 9. В таком случае говорят, что выражение 5х + 2х — 9 заменили тождественным ему выражением 7х — 9.
Тождественные преобразования выражений с переменными выполняют, применяя свойства действий над числами. В частности, тождественными преобразованиями с раскрытие скобок, возведение подобных слагаемых и тому подобное.
Тождественные преобразования приходится выполнять при упрощении выражения, то есть замены некоторого выражения на тождественно равное ему выражение, которое должно короче запись.
Пример 1. Упростить выражение:
1) -0,3 m ∙ 5n = -0,3 ∙ 5mn = -1,5 mn;
2) 2(3х 4) + 3( -4 + 7) = 6x — 8 — 12х + 21 = 6x + 13;
3) 2 + 5а — (а — 2b) + (3b — a) = 2 + 5а — а + 2b + 3b — а = 3а + 5b + 2.
Чтобы доказать, что равенство является тождеством (иначе говоря, чтобы доказать тождество, используют тождественные преобразования выражений.
Доказать тождество можно одним из следующих способов:
- выполнить тождественные преобразования ее левой части, тем самым сведя к виду правой части;
- выполнить тождественные преобразования ее правой части, тем самым сведя к виду левой части;
- выполнить тождественные преобразования обеих ее частей, тем самым возведя обе части до одинаковых выражений.
Пример 2. Доказать тождество:
2) 206 — 4а = 5(2а — 3b) — 7(2а — 5b);
3) 2(3x — 8) + 4(5х — 7) = 13(2x — 5) + 21.
1) Преобразуем левую часть данного равенства:
2х — (х + 5) — 11 = 2х — х — 5 — 11 = х — 16.
Тождественными преобразованиями выражение в левой части равенства свели к виду правой части и тем самым доказали, что данное равенство является тождеством.
2) Преобразуем правую часть данного равенства:
5(2а — 3b) — 7(2а — 5b) = 10а — 15b — 14а + 35b = 20b — 4а.
Тождественными преобразованиями правую часть равенства свели к виду левой части и тем самым доказали, что данное равенство является тождеством.
3) В этом случае удобно упростить как левую, так и правую части равенства и сравнить результаты:
2(3х — 8) + 4(5х — 7) = 6х — 16 + 20х — 28 = 26х — 44;
13(2х — 5) + 21 = 26х — 65 + 21 = 26х — 44.
Тождественными преобразованиями левую и правую части равенства свели к одному и тому же виду: 26х — 44. Поэтому данное равенство является тождеством.
Какие выражения называют тождественными? Приведите пример тождественных выражений. Какое равенство называют тождеством? Приведите пример тождества. Что называют тождественным преобразованием выражения? Как доказать тождество?
- (Устно) Или есть выражения тождественно равными:
- Являются ли тождественно равными выражения:
- (Устно) является Ли тождеством равенство:
источник
Доказательство тригонометрических тождеств
При доказательстве любых тождеств, и в частности тригонометрических, обычно используют следующие способы:
1) выражение, стоящее и одной части равенства, с помощью тождественных преобразований приводят к выражению, стоящему в другой части равенства;
2) выражения, стоящие в левой и правой частях тождества, с помощью тождественных преобразований приводят к одному и тому же виду;
3) доказывают, что разность между левой и правой частями данного тождества равна нулю.
Поясним это на некоторых частных примерах.
Пример 1. Доказать тождество
sin 4 α — cos 4 α = sin 2 α — cos 2 α .
Используя формулу для разности квадратов двух чисел, получаем:
sin 4 α — cos 4 α = (sin 2 α + cos 2 α) (sin 2 α — cos 2 α).
Ho sin 2 α + cos 2 α = 1. Поэтому
sin 4 α — cos 4 α = sin 2 α — cos 2 α, что и требовалось доказать.
Пример 2. Доказать тождество
Это тождество мы будем доказывать путем преобразования выражения, стоящего в правой части.
Поэтому
Прежде всего заметим, что ctg α =/= 0; в противном случае не имело бы смысла выражение tg α = 1 /ctgα. Но если ctg α =/= 0, то числитель и знаменатель подкоренного выражения можно умножить на ctg α, не изменяя значения дроби. Следовательно,
Используя тождества tg α • ctg α = 1 и 1+ ctg 2 α = cosec 2 α , получаем
Поэтому что и требовалось доказать.
Замечание. Следует обратить внимание на то, что левая часть доказанного тождества (sin α) определена при всех значениях α, а правая — лишь при α =/= π /2 n.
Поэтому только при всех допустимых значениях α Вообще же эти выражения не эквивалентны друг другу.
Пример 3. Доказать тождество
Преобразуем левую и правую части этого тождества, используя формулы приведения:
Итак, выражения, стоящие в обеих частях данного тождества, приведены к одному и тому же виду. Тем самым тождество доказано.
Пример 4. Доказать тождество
Покажем, что разность между левой и правой частями. данного тождества равна нулю.
= (sin 2 α + cos 2 α) 2 — 1 = 1 — 1 = 0.
Тем самым тождество доказано.
Пример 5. Доказать тождество
Это тождество можно рассматривать как пропорцию. Но чтобы доказать справедливость пропорции a /b = c /d, достаточно показать, что произведение ее крайних членов ad равно произведению ее средних членов bc. Так мы поступим и в данном случае. Покажем, что (1 — sin α) (1+ sin α) = cos α • cos α.
По поводу этого примера можно было бы сделать замечание, аналогичное замечанию к примеру 2.
1). Найти значение выражения , если известно, что tg α = 1 /3
2). Найти значение выражения , если известно, что котангенс угла α не определен.
3). Найти значение выражения , если известно, что ctg α = 1 /2
источник
Открытый урок в рамках системно-деятельностного подхода. Тип урока: изучение нового материала
| Вложение | Размер |
|---|---|
| конспект открытого урока | 55.5 КБ |
| раздаточный материал к открытому уроку | 37.5 КБ |
| презентация к открытому уроку | 140.5 КБ |
Учитель: Афонасова Ирина Олеговна
Тип урока: изучение нового материала
Тема: Доказательство тождеств
- Повторить определения тождества и тождественно равных выражений, тождественного преобразования выражений.
- Формирование навыка выбора способа доказательства тождеств методом тождественного преобразования выражений.
- Воспитывать коммуникативную культуру учащихся.
1 . Организационный этап урока
Перед началом урока учащиеся класса разбиваются на шесть учебных групп смешанного состава.
Учитель : Здравствуйте, ребята, я предлагаю учебный кабинет превратить на время в научно-исследовательскую лабораторию , а нам с вами в ученых-магистров математических наук .
Но каждый, уважающий себя ученый, постоянно решает какую-нибудь очень важную проблему, вот и нам, прежде всего, предстоит узнать: над какой проблемой мы будем сегодня работать?
Для этого рассмотрим выражения 2х+у и 2ху. Найдём значения выражений при х=1 и у=2.
Учител ь предлагает выйти к доске учащемуся и решить данную задачу, а также сформулировать вывод : при х=1 и у=2 выражения принимают равные значения (4).
Учитель: Однако можно указать такие значения переменных х и у, при которых значения этих выражений не равны. Например, х=3, у=4.
Ученик , стоящий у доски, проверяет это.
Учитель: Рассмотрим теперь выражения 3(х+у) и 3х+3у. Найдём значения выражений при х=5 и у=4.
Ученик, стоящий у доски: решает задачу, формулирует вывод.
Учитель: При любых ли значениях переменных значения данных выражений равны? Если да, то почему?
Ученик отвечает. (Ответ: Да, по распределительному свойству умножения).
Учитель предлагает классу вспомнить название таких выражений, название их равенства.
Следом за тем учитель спрашивает: «Какова тема сегодняшнего урока».
Учитель : Работать сегодня мы будем над «Доказательством тождеств».
Записывается тема урока: «Доказательство тождеств» ( Слайд2 )
Учитель : Хорошо, а сейчас проверим себя. На экране будут появляться равенства, если это равенство будет являться тождеством, то я предлагаю вам поднять руку. ( Слайд 3 )
- — (а – в) = — а + в (да)
- а (в + с) = ав – ас (нет)
- а – (в + с) = а – в + с (нет)
- (а + в) – с = а – с + в (да)
- — (а + в) = — а – в (да)
Учитель : Хорошо, а сейчас пришла пора из теоретиков нам превращаться в ученых- практиков, но для этого нам нужно узнать, что нужно использовать, чтобы доказать тождество , и здесь нам не обойтись без научной литературы, ответ на этот вопрос мы найдем на странице 18 вашего учебника. Учащиеся находят в учебнике ответ: «Чтобы доказать, что некоторое равенство является тождеством, используют тождественные преобразования выражений» . Согласие или несогласие участники остальных групп показывают специальными сигналами, о которых говорилось выше. ( Слайд 4 )
Учитель : Молодцы, но теперь возникает следующий вопрос, а что такое тождественное преобразование выражений ?
«Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения» (учитель предлагает ответить на этот вопрос одного из участников любой группы) ( Слайд 5 )
Учитель : Итак, какова цель урока? Учащиеся называют одну из поставленных целей: научиться доказывать тождества, используя тождественные преобразования выражений.
4. Выявление способа доказательства тождеств методом тождественного преобразования выражений
Учитель: Вот сейчас мы уже «созрели» для практической работы, и я попрошу вас обратить свое внимание на карточку . Задание: «Докажите тождество», каждая группа ученых получила пример, который она должна решить самостоятельно, если будут возникать затруднения на помощь придут карточки- консультанты.
источник
! 
A \ B = A \ B = A 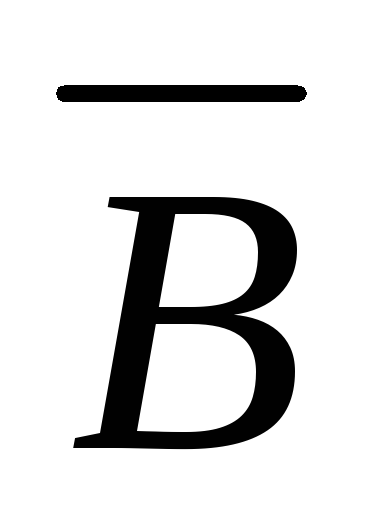
B \ A = B \ A = B 
Замечание. Отношения включения множеств могут быть определены в терминах и .
Следующие утверждения о произвольных множествах А и В попарно эквивалентны:
А
С помощью законов алгебры множеств можно упрощать выражения, содержащие множества.
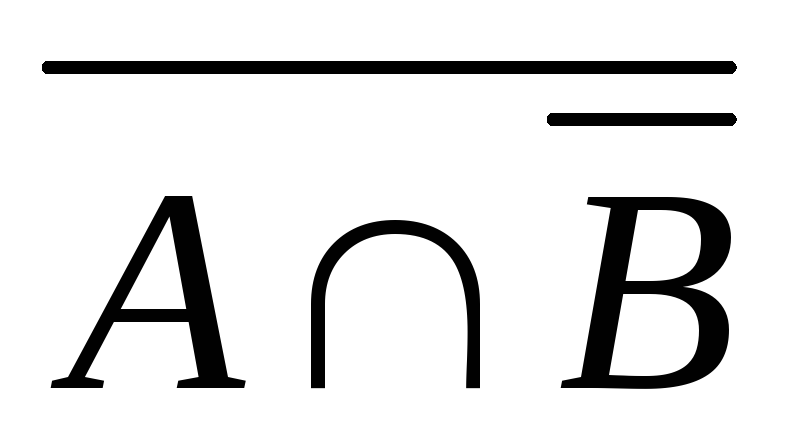





(A \ B) (A B) = (A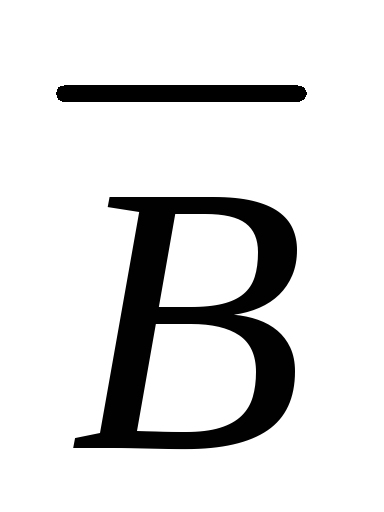
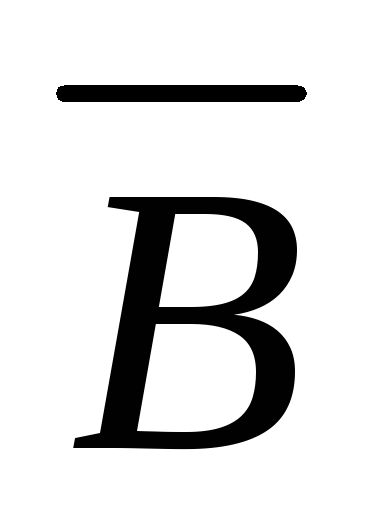
а) A (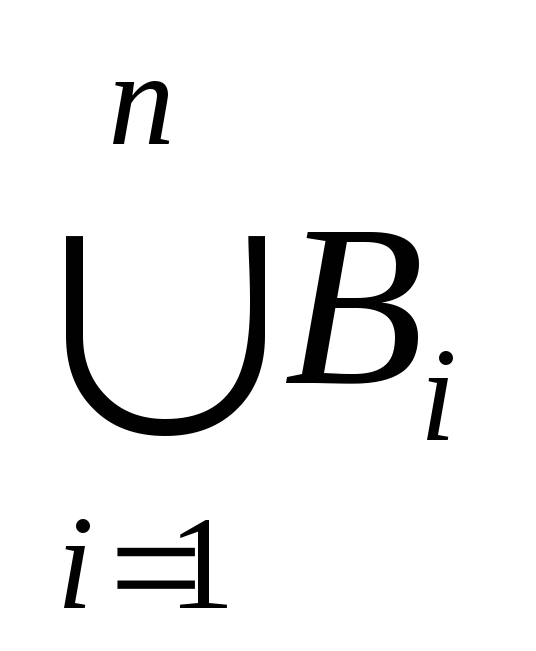
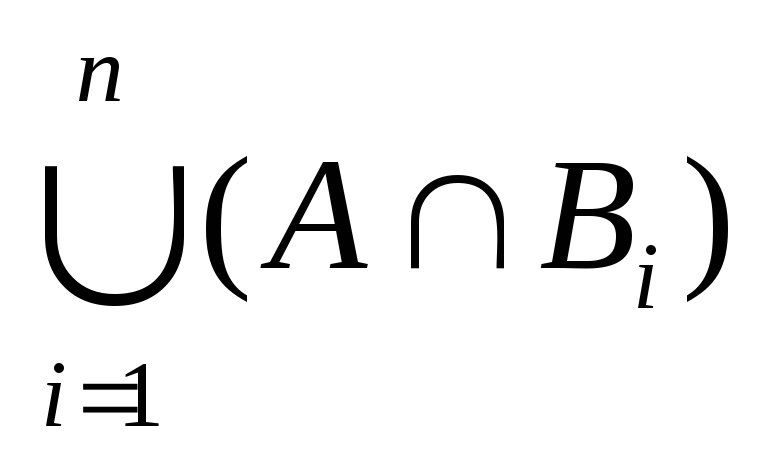
б) A (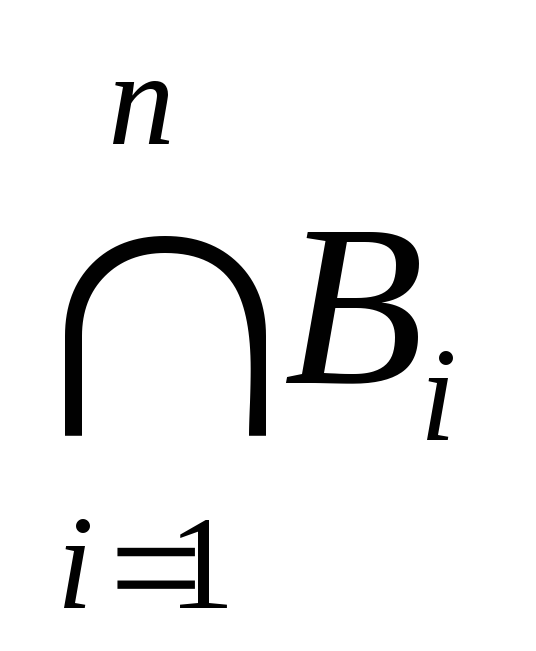
Доказательство утверждения (а) (методом математической индукции):
правая часть (1) = (AB1)(AB2) левая часть=правая часть (по доказанному ранее закону дистрибутивности пересечения относительно объединения).
2) Допустим, формула (а) верна при каком-то произвольном натуральном n=k (k2), т.е. допустим, что справедливо равенство: A(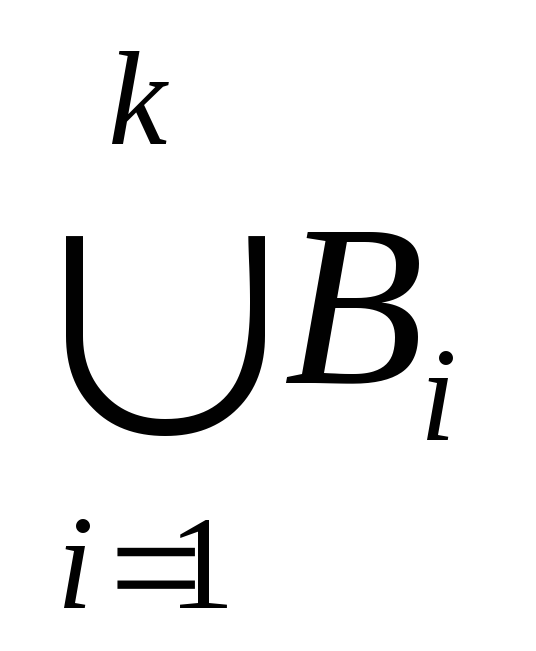
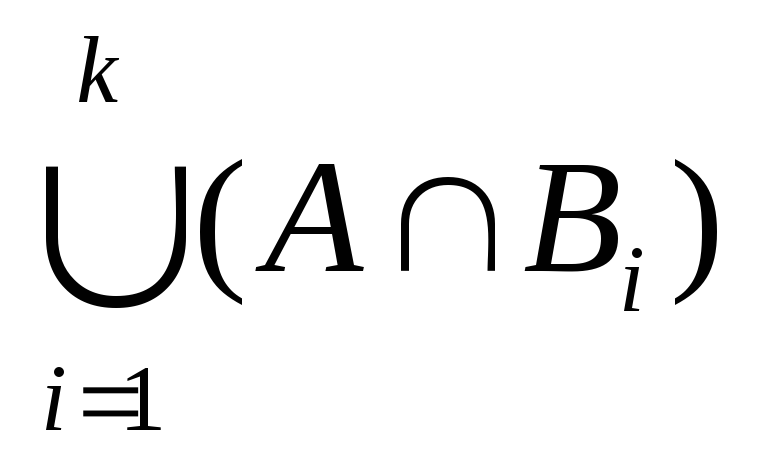
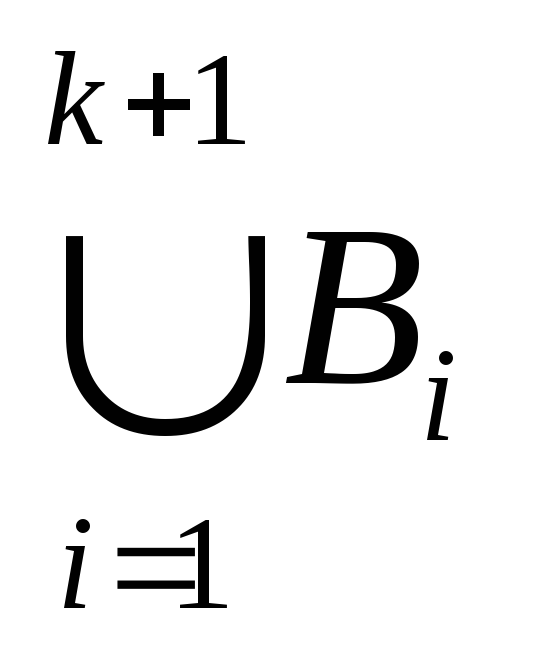
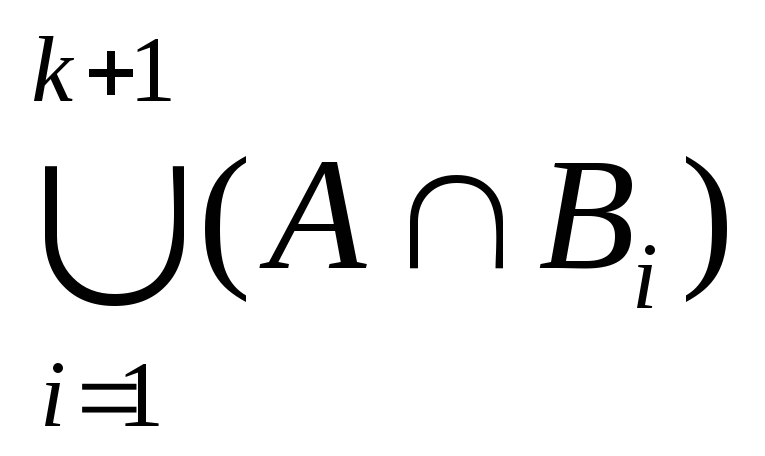
Доказательство: A (
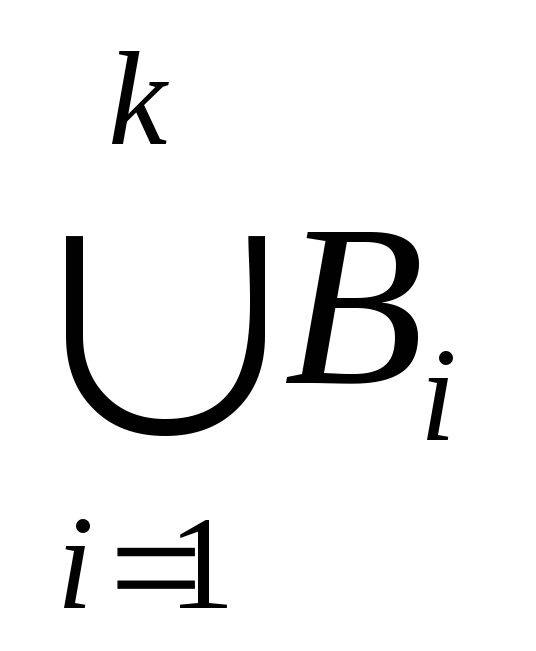
= (A (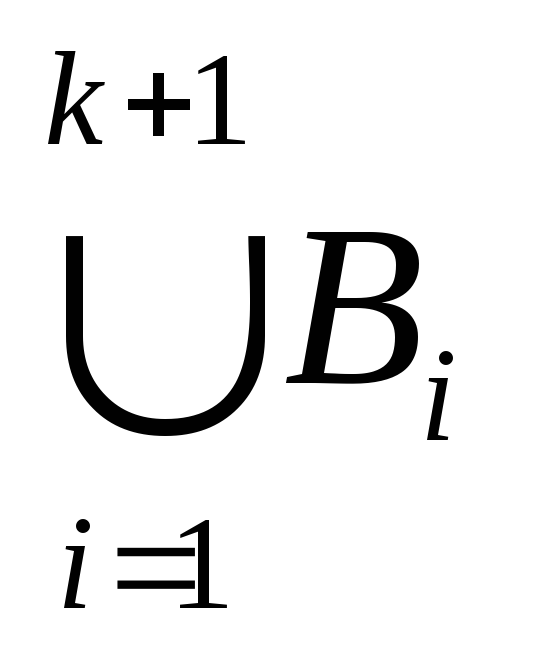
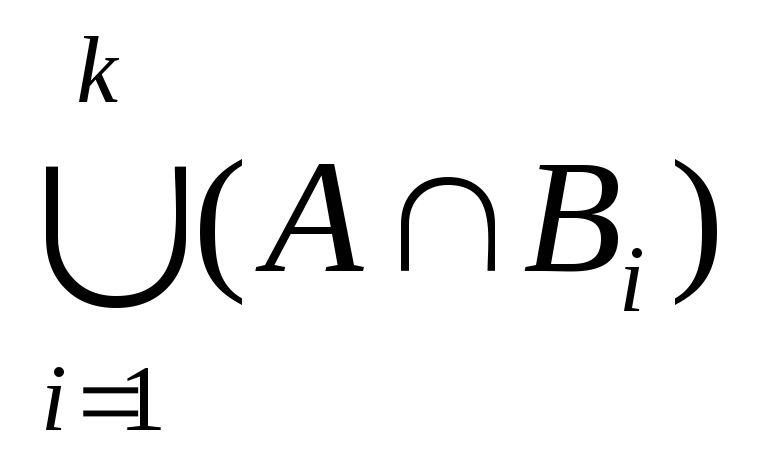
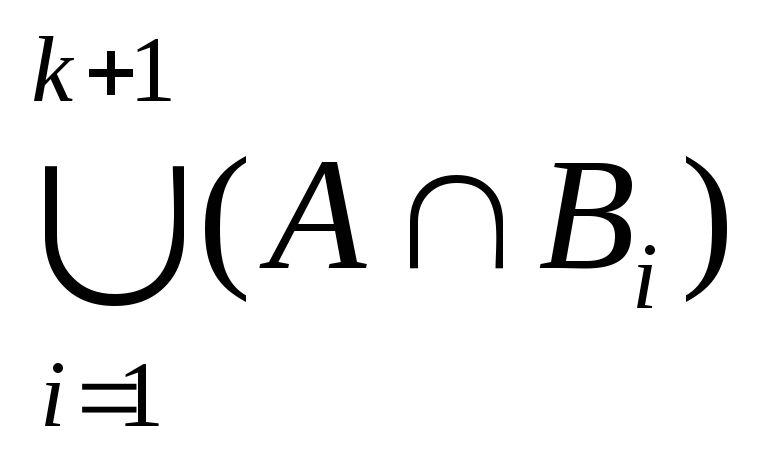
Так как утверждение (а) верно при n=2 и из истинности его при каком-то произвольном натуральном n=k (k 2) следует его справедливость и при следующем n=k+1, то равенство (1) верно для всех натуральных n2 на основании обобщенного принципа математической индукции.
Обобщенный закон де Моргана
а) 
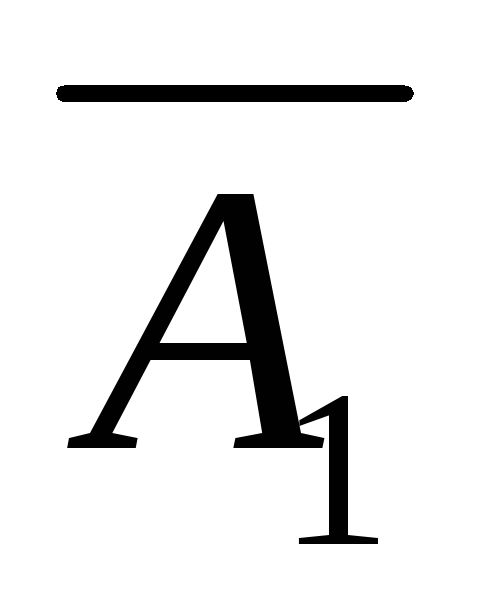

б) 
Доказательство утверждения (а) (методом математической индукции):
1) n = 2: левая часть = 
правая часть = 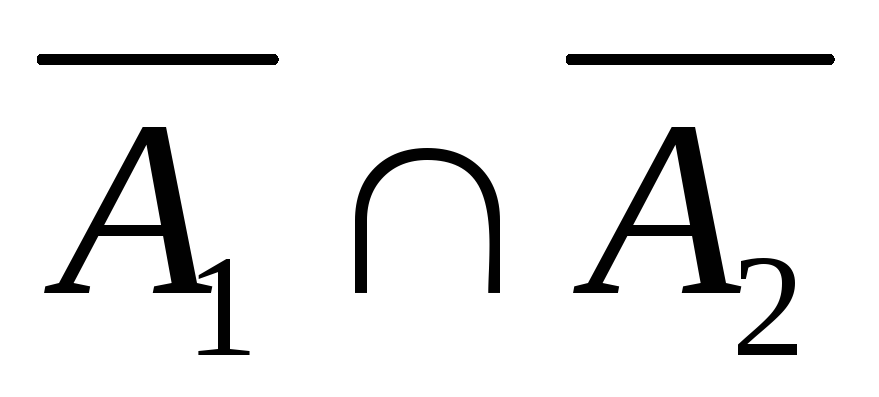
2) Допустим: 

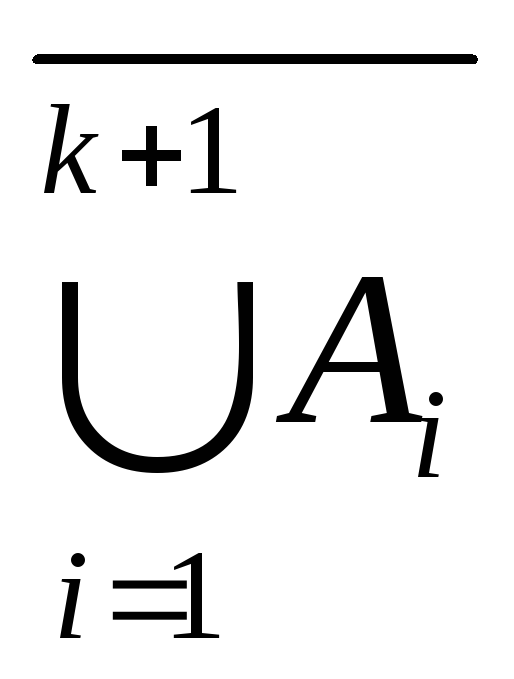
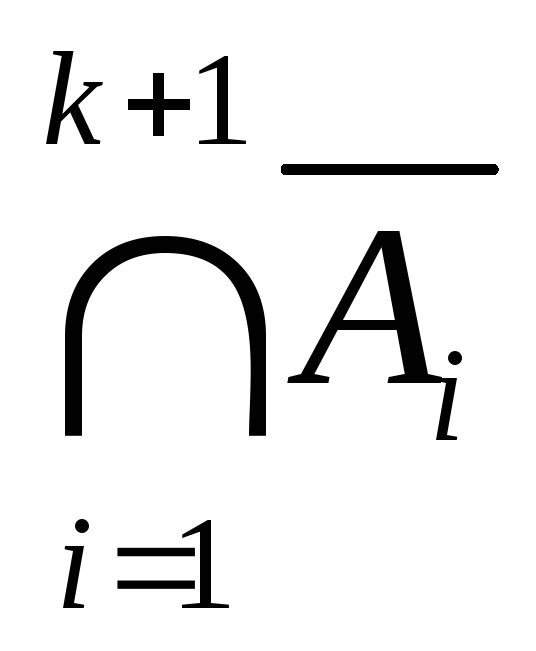
Доказательство: 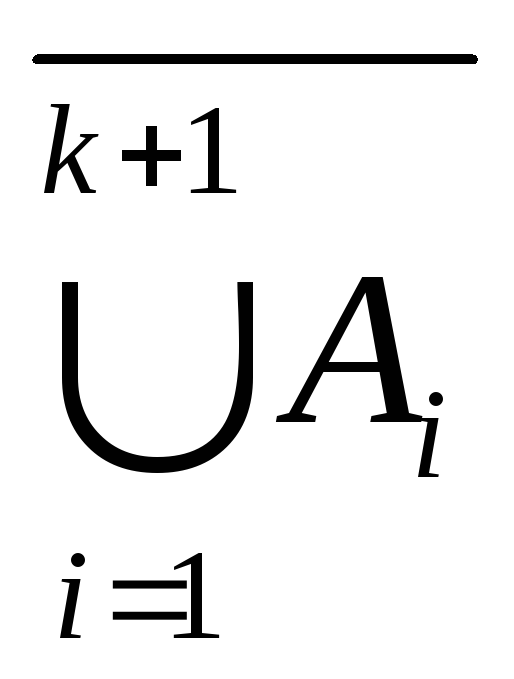
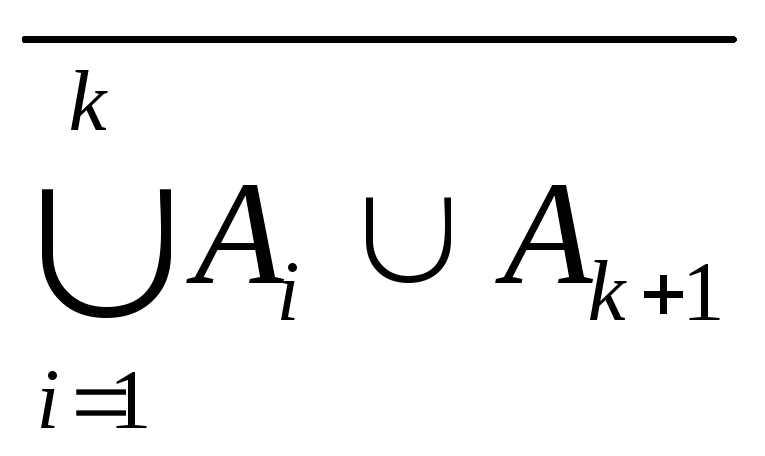
= 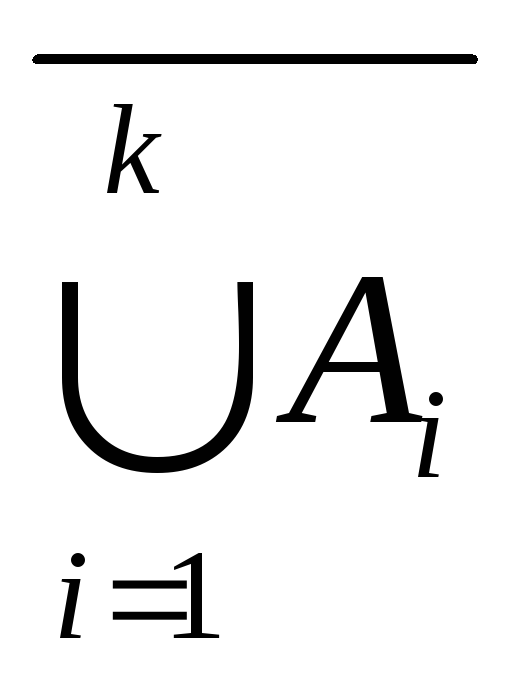
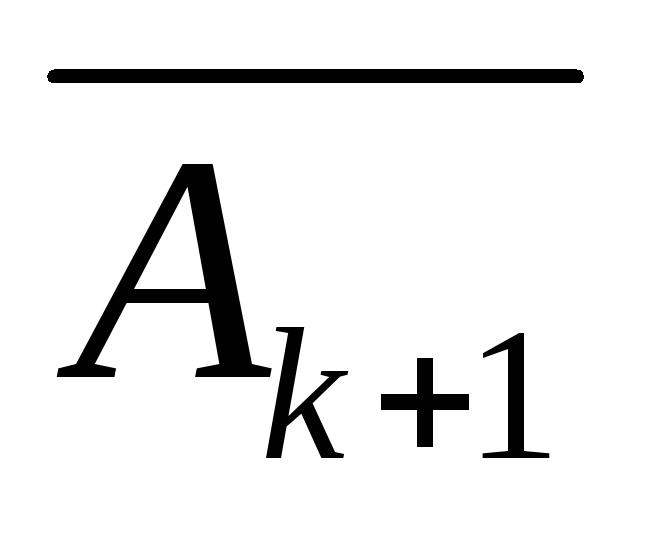



Так как выполнены оба условия обобщенного принципа математической индукции, то равенство (1) верно для всех натуральных n2.
Мощность множества – это количество элементов множества.
В множествах A’, B’, C’ n элементов, т.е. | A’| = |B’| = |C’| = n
Определение 1.15. Между множествами А и В установлено взаимно-однозначное соответствие, если элементы этих множеств объединены в пары и каждый элемент попал в одну и только одну пару.
Определение 1.16. Два множества (конечных или бесконечных) имеют одинаковую мощность, если между этими множествами можно установить взаимно-однозначное соответствие.
Определение 1.17. Множество бесконечно тогда и только тогда, когда оно имеет одинаковую мощность с некоторым своим подмножеством, не совпадающим с самим этим множеством.
П
Определение 1.18. Множество Х называется счетным, если его мощность равна мощности множества натуральных чисел, т.е. |X| = |N|.
Пример: Натуральные и целые числа равны по мощности! Равенство |N| = |Z| докажем установлением следующего соответствия: n
Утверждения о счетности множеств:
Любое подмножество счетного множества не более чем счетно.
Объединение счетного множества конечных множеств счетно.
Объединение счетного или конечного числа счетных множеств счетно.
Определение 1.19. Мощность множества А меньше мощности множества В (|A| |N|.
Доказательство: От противного. Допустим, отрезок [0; 1] – счетное множество. Значит, существует его нумерация. Расположим все числа, изображенные бесконечными десятичными дробями в порядке этой нумерации:
Рассмотрим любую бесконечную десятичную дробь 0, b1b2b3 … такую, что b1a11, b2a22, b3a33 и т.д. Эта дробь не может войти в указанную последовательность, т.к. от 1-го числа она отличается 1-ой цифрой после запятой, от 2-го – 2-ой цифрой и т.д. Следовательно, все числа из [0; 1] не могут быть пронумерованы. Значит, предположение от счетности отрезка [0; 1] неверно.
Замечание. Используемый в доказательстве метод рассуждений получил название диагонального метода Кантора.
Определение 1.20. Мощность отрезка [0; 1] называется континуумом. Множество такой мощности называется континуальным.
источник
“Математическая истина, независимо
от того, в Париже или в Тулузе, одна и та же”
Б. Паскаль
Тип урока: Урок формирования умений и навыков.
Урок общеметодологической направленности.
Деятельностная цель: формирование способности учащихся к новому способу действия, связанному с построением структуры изученных понятий и алгоритмов.
- дидактическая: научить применять полученные ранее знания, умения и навыки для упрощения выражений и доказательства тригонометрических тождеств.
- развивающая: развивать логическое мышление, память, познавательный интерес, продолжать формирование математической речи, вырабатывать умение анализировать и сравнивать.
- воспитательная: показать, что математические понятия не изолированы друг от друга, а представляют определенную систему знаний, все звенья которой находятся во взаимной связи, продолжить формирование эстетических навыков при оформлении записей, навыков контроля и самоконтроля.
Для успешного решения задач по тригонометрии необходимо уверенное владение многочисленными формулами. Тригонометрические формулы надо помнить. Но это не значит, что их надо заучивать все наизусть, главное запоминать не сами формулы, а алгоритмы их вывода. Любую тригонометрическую формулу можно довольно быстро получить, если твердо знать определения и основные свойства функций sinα , cosα , tgα , ctgα ,соотношение sin 2 α + cos 2 α =1 и т.д.
Разучивание тригонометрических формул в школе не для того чтобы вы всю оставшуюся жизнь вы вычисляли синусы и косинусы, а для того чтобы ваш мозг приобрел способность работать. (Презентация. Слайд 2)
“Дороги не те знания, которые отлагаются в мозгу, как жир; дороги те, которые превращаются в умственные мышцы” писал Г. Спесер, английский философ и социолог.
Будем накачивать и тренировать умственные мышцы. Поэтому повторим основные тригонометрические формулы. (Слайд 3)
Мы повторили формулы, теперь можем помочь двум друзьям, назовём их Пётр и Степан.
После преобразования некоторого очень сложного тригонометрического выражения А они получили следующие выражения: (Слайд 6)
(Слайд 7) Каждый отстаивал свой ответ. Как узнать кто из них прав? Обратились к Артёму, который дружит с Петром “Платон мне друг, но истина дороже”: сказал Артём и предложил несколько способов разрешения их спора. А какие вы можете предложить способы установить истину? Предлагают способы установления истины (Слайд 8):
1) Преобразовать, упростить А П и Ас, т.е. привели к одному выражению
Т. е. оба были правы. И их ответы равны при всех допустимых значениях α и β .
Как называются такие выражения? Тождествами. Какие тождества вы знаете?
Тождество, основное понятие логики, философии и математики; используется в языках научной теорий для формулировки определяющих соотношений, законов и теорем.
Тождество – философская категория, выражающая равенство, одинаковость предмета, явления самим с собой или равенство нескольких предметов.
В математике тождество – это равенство, которое справедливо для любых допустимых значений входящих в него переменных. (Слайд 9)
Тема урока: “Тригонометрические тождества”.
Способы доказательства тождеств.
- Выполнить равносильные преобразования правой части тождества. Если в итоге получим левую часть, тогда тождество считается доказанным.
- Выполнить равносильные преобразования левой и правой части тождества. Если в результате получим одинаковый результат, тогда тождество считается доказанным.
- Из правой части тождества вычитаем левую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным.
- Из левой части тождества вычитают правую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным.
Следует так же помнить, что тождество справедливо лишь для допустимых значений переменных.
Для чего необходимо уметь доказывать тригонометрические тождества? В ЕГЭ задание С1 тригонометрические уравнения!
Итак, подведем итоги урока. (Слайд 10)
Какие способы доказательства тождеств вам известны?
1. Преобразование левой части к правой или правой к левой.
2. Преобразование левой и правой части к одному и тому же выражению.
3. Составление разности левой и правой частей и доказательство равенства этой разности нулю.
Какие формулы при этом используются?
1. Формулы сокращенного умножения.
2. 6 тригонометрических тождеств.
– сегодня на уроке я узнал …
– сегодня на уроке я научился…
– сегодня на уроке я повторил…
– сегодня на уроке я познакомился…
– сегодня на уроке мне понравилось…
Домашнее задание. Глава VIII; §6; № 78(четные); № 80(2; 4); № 87(2; 4). (Слайд 12)
Творческое задание: Подготовить презентацию о знаменитых тождествах математики. (Например тождество Эйлера.) (Слайд 13)
источник
‘ способами. Спикер включается в делегацию только в том случае, когда в ней нечетное число «рядовых» депутатов. Таким образом, общее число делегаций с четным числом членов равно 2п
1, Поскольку обшее число подмножеств есть 2П, подмножеств с нечетным числом элементов также 2П_|, то есть столько же, сколько и с четным числом элементов. Значит, поскольку части записанного равенства выражают собой число подмножеств n-элементного множества соответственно с нечетным и четным числом элементов. Полученное равенство равносильно доказываемому. 5) Данное соотношение является другой формой записи предыдущего тождества. Комбинаторные тождества 6) Решим такую задачу. Имеется т мужнин и п женщин. Из них нужно сформировать делегацию из к человек. Каким числом способов это можно сделать? Отвег очевиден: с£+п. Будем классифицировать делегации по числу мужчин. Если в делегацию входят з мужчин и k — а женщин, то мужчин можно выбрать способами, а женшин — способами; значит, число делегаций с з > мужчинами равно . Суммируя
a по s от 0 до к, получим обшее число делегаций. 7) Для доказательства достаточно в предыдущем соотношении положить применить 1). 8) Доказательство тождества может быть получено из решения следующей задачи: Каким числом способов можно из п кандидатов выбрать к депутатов и среди последних спикера? Депутаты выбираются С£ способами, после чего спикер выбирается к способами; таким образом, общее число способов равно С„ к. То же число можно подсчитать по-другому. Будем сначала (всенародным голосованием) избирать спикера (из п кандидатов), а затем из оставшихся п — 1 кандидата — еще депутата. Указанная процедура может быть выполнена п • J способами. Доказано, что . Отсюда вытекает полезное рекуррентное соотношение , применяя которое несколько (точнее: к) раз, можно вновь вывести формулу для числа сочетаний 9) Это тождество — обобщение предыдущего (если в 9) положить m = 1, то получим 8)) и может быть доказано с помощью решения задачи, таюсе являющейся обобщением ранее рассмотредаой: Каким числом способов можно выбрать из п кандидатов к депутатов и среди последних т членов президиума? 10) 1-й способ. Докажем тождество математической индукцией по к. База индукции. При к = 0 имеем верное равенство: Индукционный шаг. Пусть доказываемое утверждение верно при : Прибавив к обеим частям равенства , получим Таким образом, соотношение 10) справедливо и при . 2-й способ. Общее число (-элементных подмножеств множества равно , (правой части доказываемого тождества). Будем классифицировать указанные подмножества по их наибольшему элементу, который, очевидно, принимает значения . Найдем число подмножеств с наибольшим элементом т+р 4-1. Поскольку наибольший элемент уже выбран, оставшиеся m элементов выбираются из множества значит, число таких подмножеств равно Суммируя , вновь получим общее число -элементных подмножеств (левую часть доказываемого тождества). 11) Тождество доказывается на основе предыдущего: 12) Решим задачу: Каким числом способов можно из п кандидатов выбрать т депутатов и среди депутатов некоторых (может быть, всех, а может быть, никого) наградить ? С одной стороны, депутаты выбираются способами, а награжденные выделяются 2т способами (столько подмножеств имеет множество из m элементов), и, значит, ответ к задаче: . С другой стороны, если число награждаемых депутатов равно к , то их можно выбрать способами, после чего остальные m — к депутатов выбираются способами. Суммируя по к от 0 до тп, вновь Комбинаторные тождества получим ответ к рассматриваемой задаче. Тождество доказано. 13) Используя соотношение 8), преобразуем общий член суммы: 2-й способ. Воспользовавшись 13) тождеством, заметм и в полученной двойной сумме поменяем порядок суммирования
Информация расположенная на данном сайте несет информационный характер и используется для учебных целей.
© Брильёнова Наталья Валерьевна
источник
Требенкова Л. М., учитель математики.
Данная статья представляет собой разработку урока по алгебре 7 класса по теме «Доказательство тождеств». Урок проводится в групповой форме, сопровождается электронной презентацией. Для активизации мыслительной деятельности учащихся применяется игровой прием, работа в научно-исследовательской лаборатории.
1. Повторить определения тождества и тождественно равных выражений.
2.Ввести понятие тождественного преобразования выражений.
3. Развивать у учащихся навыки доказательства тождеств методом тождественного преобразования выражений.
4. Воспитывать коммуникативную культуру учащихся.
Перед началом урока учащиеся класса разбиваются на шесть учебных групп смешанного состава.
1. Учитель: Здравствуйте, ребята, я предлагаю учебный кабинет превратить на время в научно- исследовательскую лабораторию, а нам с вами в ученых- магистров математических наук.
Но каждый, уважающий себя ученый, постоянно решает какую-нибудь очень важную проблему, вот и нам, прежде всего, предстоит узнать: над какой проблемой мы будем сегодня работать?
Для этого нам нужно решить две задачи: (Слайд №1)
1) Разложите на множители выражение 4х – 8ху. (После выполнения задания на слайде появляется слово «Доказательство»)
2) Представьте выражение -5у( у – 2) в виде многочлена. (После выполнения задания на слайде появляется слово «Тождеств»)
Учитель: Работать сегодня мы будем над «Доказательством тождеств», а девизом нашей работы я предлагаю взять вот эти замечательные слова: (Слайд №2)
Пусть каждый день и каждый час
Пусть добрым будет ум у нас,
2. Учитель: Господа ученые, прежде чем решать поставленную задачу, нам необходимо укрепить свою теоретическую базу, ведь понятие тождества вам уже знакомо. И поэтому в рубрике (Слайд №3) « Повторение – мать учения» я предлагаю вам провести следующую работу:
В каждой научной группе находятся формулировки трех понятий на карточке №1, вы должны среди них найти два определения: 1) Определение тождества, 2) Определение тождественно равных выражений.
( Учащиеся в течение 2- 3 минут изучают эти определения, спрашиваются представители тех групп, которые быстрее всех справились с заданием, остальные участники других групп показывают согласие или несогласие с помощью сигнальных карточек зеленого и красного цветов)
……… — это равенство, верное при любых допустимых значениях, входящих в его состав переменных.
Два выражения, соответственные значения которых равны при любых значениях переменных, называются ……….. равными.
Замену одного выражения другим, тождественно равным ему, называют………… преобразованием выражения.
После того как учащиеся дают верное определение, оно высвечивается на экране.
Учитель: Хорошо, а сейчас проверим себя. На экране будут появляться равенства, если это равенство будет являться тождеством, то я предлагаю вам встать, если же – нет, то вы продолжаете сидеть: (Слайд №4)
3. Учитель: Хорошо, а сейчас пришла пора из теоретиков нам превращаться в ученых- практиков, но для этого нам нужно узнать, что нужно использовать, чтобы доказать тождество, и здесь нам не обойтись без научной литературы, ответ на этот вопрос мы найдем на странице…………… вашего учебника. Учащиеся находят в учебнике ответ: «Чтобы доказать, что некоторое равенство является тождеством, или, как говорят иначе, чтобы доказать тождество, используют тождественные преобразования выражений». Согласие или несогласие участники остальных групп показывают специальными сигналами, о которых говорилось выше. (Слайд №5)
Учитель: Молодцы, но теперь возникает следующий вопрос, а что такое тождественное преобразование выражений? Ответ можно найти на карточке №1, это оставшееся третье определение.
« Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения» (учитель предлагает ответить на этот вопрос одного из участников любой группы) (Слайд №6)
Вот сейчас мы уже «созрели» для практической работы, и я попрошу вас обратить свое внимание на карточку №2. Задание: «Докажите тождество», каждая группа ученых получила пример, который она должна решить самостоятельно, если будут возникать затруднения на помощь придут карточки- консультанты.
Выпишите выражение в левой части указанного равенства, раскрой те скобки и приведите подобные слагаемые, сравните полученное выражение с выражением правой части, сделайте вывод.
2. 5х – 7 = 28х – 3 – х — 4 – 22х
Выпишите выражение правой части указанного равенства, приведите подобные слагаемые, сравните полученное выражение с выражением левой части и сделайте вывод.
3. ( х – 5) ( х + 2 ) = ( х + 4 ) ( х- 7 ) + 18
Выпишите сначала выражение левой части, раскрой те скобки и приведите подобные слагаемые, затем выпишите выражение правой части, раскройте скобки и приведите подобные слагаемые. Сравните полученные выражения, сделайте вывод.
4. – (2х – 3) + (х 2 + 2х – 3) = х 2
Выпишите выражение в левой части указанного равенства, раскрой те скобки и приведите подобные слагаемые, сравните полученное выражение с выражением правой части, сделайте вывод.
Выпишите выражение правой части указанного равенства, приведите подобные слагаемые, сравните полученное выражение с выражением левой части и сделайте вывод.
6. – 4 (3у – 1 ) +1= — 6 ( 2у – 1) — 1
Выпишите сначала выражение левой части, раскрой те скобки и приведите подобные слагаемые, затем выпишите выражение правой части, раскройте скобки и приведите подобные слагаемые. Сравните полученные выражения, сделайте вывод.
Теперь нам необходимо защитить свои работы. ( Презентация выполненных работ у доски, выступают желающие участники групп)
Учитель: Замечательно, а теперь уважаемые коллеги пора подводить итоги, что же нам необходимо сделать, чтобы доказать, что равенство является тождеством? Предполагаемые ответы учащихся: (Слайд №7)
- Выписать левую часть равенства, ее преобразовать и убедиться, что она равна правой.
2. Выписать правую часть равенства, ее преобразовать и убедиться, что она равна левой.
- Преобразовать и левую и правую часть равенства и убедиться в том, что они равны одному и тому же выражению.
Учитель: Какой вывод можно сделать в том случае, когда все то, о чем мы только что сказали, не будет выполняться? Предполагаемый ответ учащихся: Равенство не будет являться тождеством.
4. Учитель: Чтобы полученные знания были прочными, эту работу мы продолжим дома:
Домашнее задание: п. 30, № 773, * Составить равенство, которое будет являться тождеством.
1. Учитель: А сейчас настал час для творчества: В стихотворении, которое вы видите, вставьте пропущенные слова: (Слайды №8, №9)
Равенства всякие, братцы, бывают,
И каждый об этом, конечно же, знает.
Есть — с переменными, есть — (числовые) ,
Сложные очень и очень (простые),
Но есть среди равенств особенный класс,
О нем поведем свой рассказ мы сейчас.
(Тождеством) равенство это зовется.
Но это еще доказать нам придется.
Для этого нужно нам только лишь взять
И равенство это (преобразовать)
Несложно, конечно, нам будет узнать
Какую придется нам часть изменять,
А, может, придется нам обе менять,
По равенства виду нетрудно (понять)
Ура! Удалось применить наши знания,
Окончено равенства преобразование.
И смело уже говорим мы ответ:
Так (тождество) это, или все-таки нет!
источник
- http://studfiles.net/preview/1901834/page:5/
- http://schooled.ru/textbook/mathematics/7klas/2.html
- http://oldskola1.narod.ru/trigF16.htm
- http://nsportal.ru/shkola/algebra/library/2013/06/19/dokazatelstvo-tozhdestv
- http://studfiles.net/preview/1901834/page:5/
- http://xn--i1abbnckbmcl9fb.xn--p1ai/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/642262/
- http://natalibrilenova.ru/blog/1505-polinomialnaya-formula.html
- http://www.schkola1zavod.ru/index/dokazatelstvo_tozhdestv/0-204