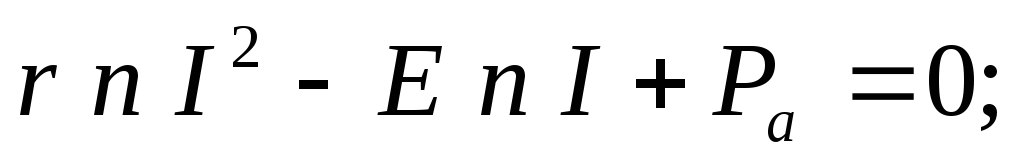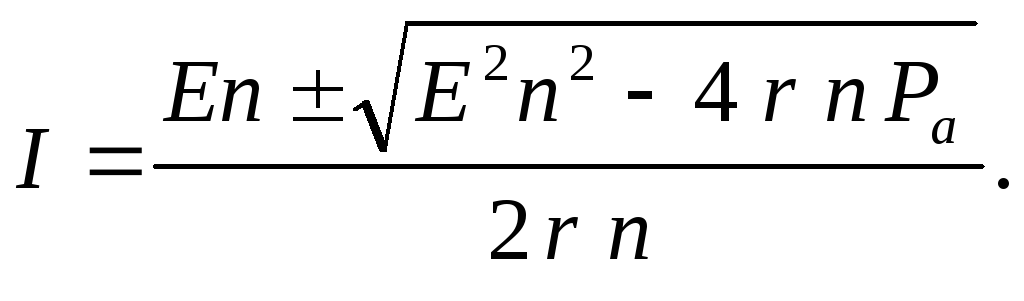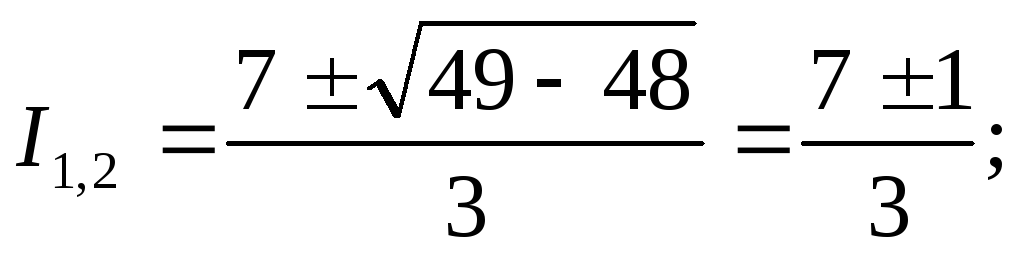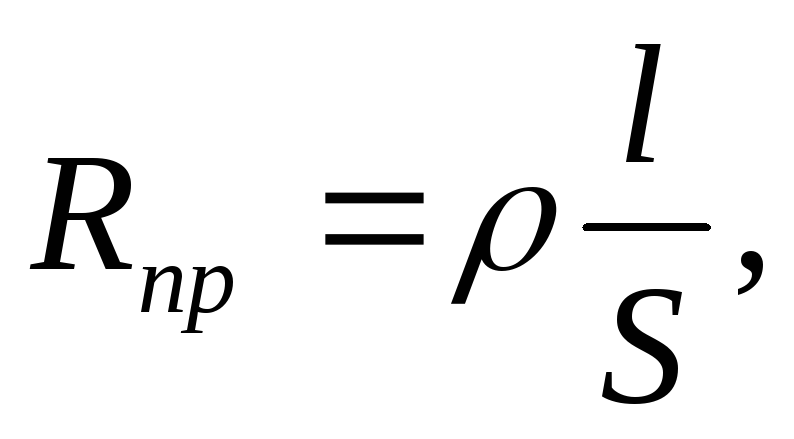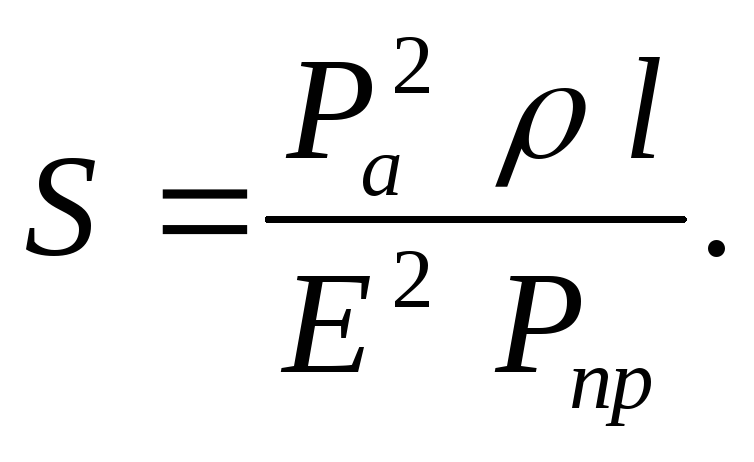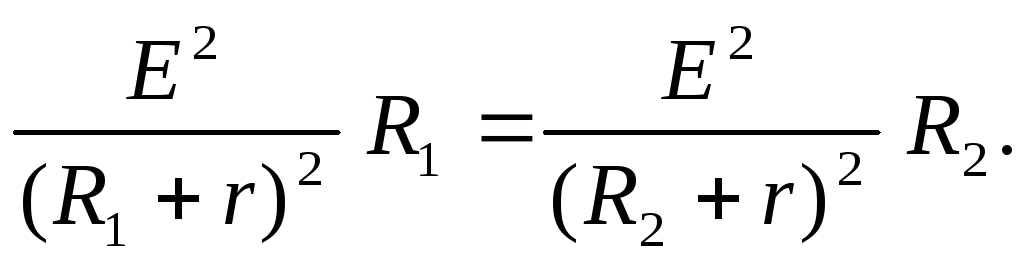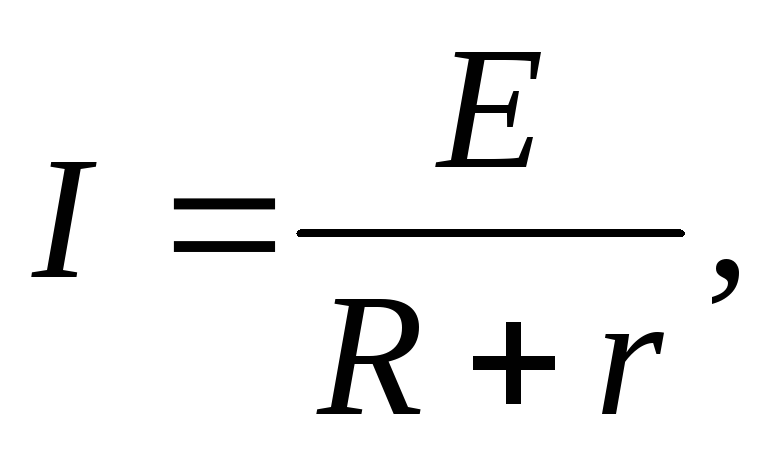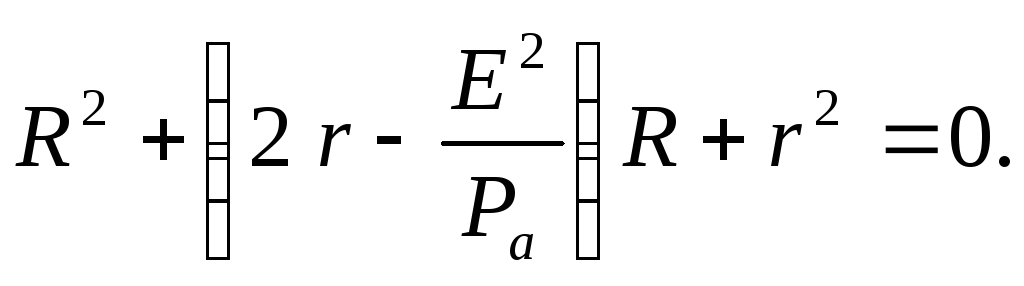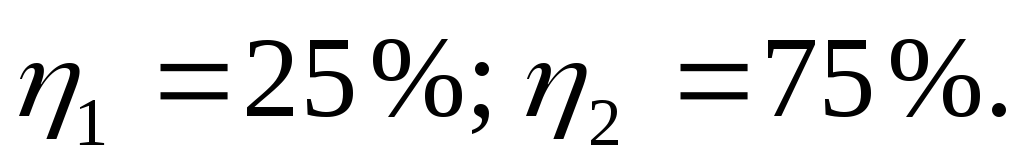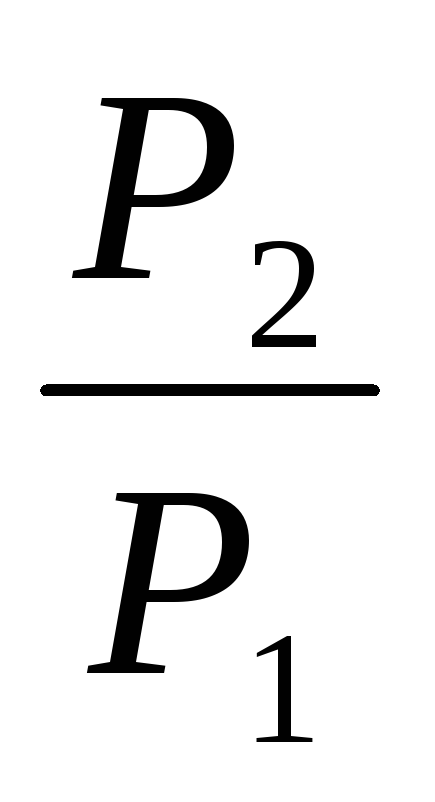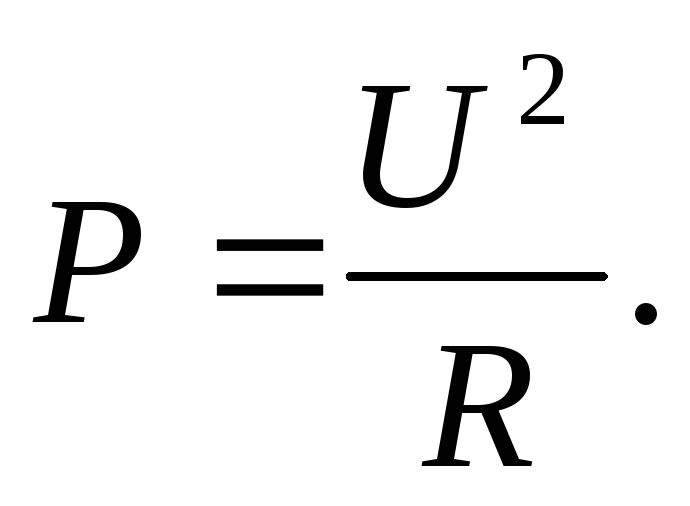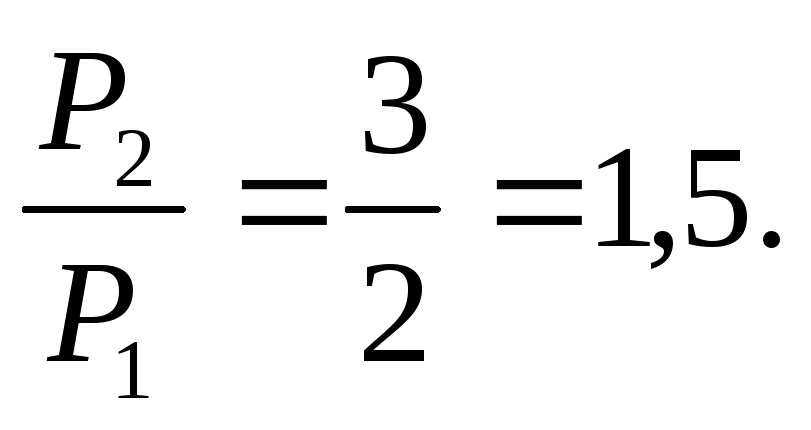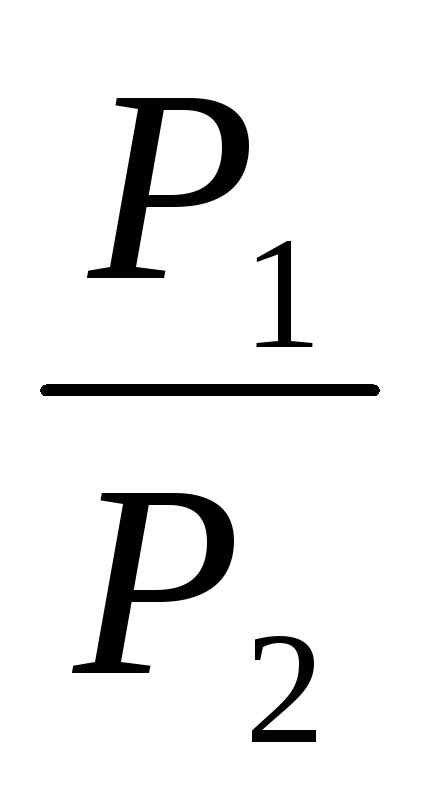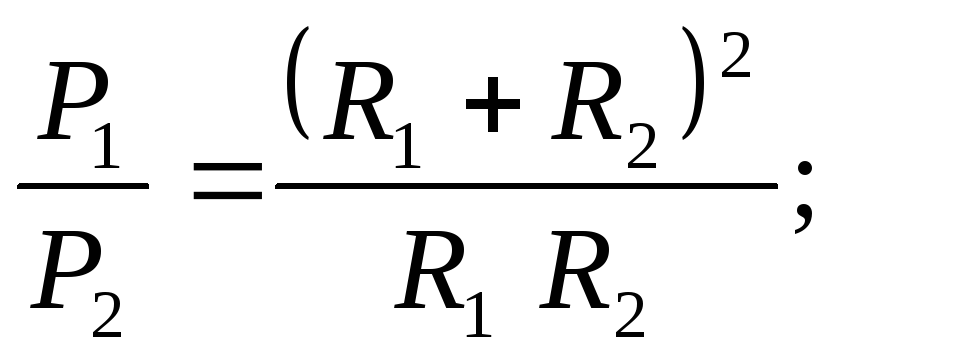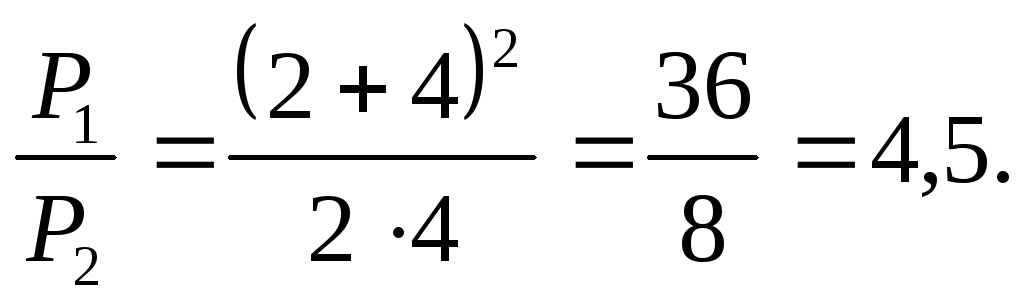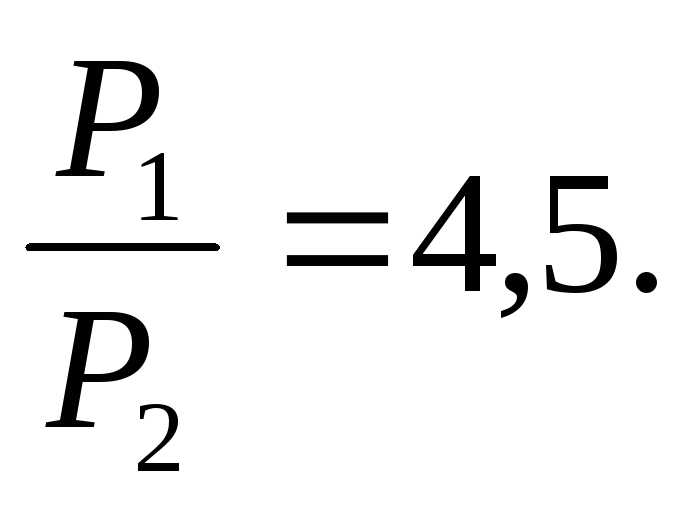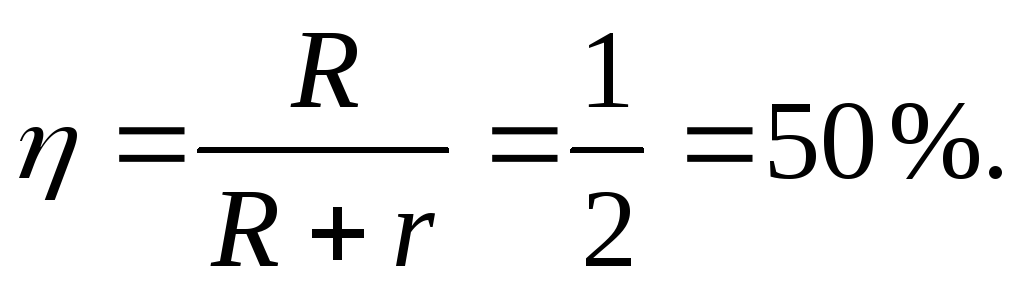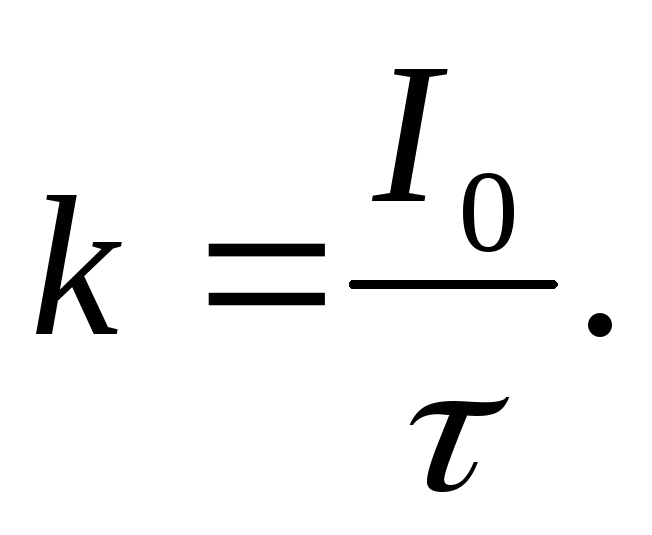Полная мощность и полезная мощность

ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ:

, (1)

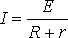
I- сила тока в цепи; Е- электродвижущая сила источника тока, включённого в цепь; R- сопротивление внешней цепи; r- внутреннее сопротивление источника тока.

. (2)

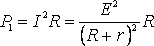
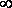
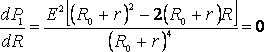
Из формулы (2) видно, что при коротком замыкании цепи (R®0) и при R®эта мощность равна нулю. При всех других конечных значениях R мощность Р₁> 0. Следовательно, функция Р₁ имеет максимум. Значение R, соответствующее максимальной мощности, можно получить, дифференцируя Р₁ по R и приравнивая первую производную к нулю:

. (3)

Из формулы (3), с учётом того, что R и r всегда положительны, а Е ? 0, после несложных алгебраических преобразований получим:

Следовательно, мощность, выделяемая во внешней цепи, достигает наибольшего значения при сопротивлении внешней цепи равном внутреннему сопротивлению источника тока.

При этом сила тока в цепи 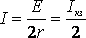(5)

равна половине тока короткого замыкания. При этом мощность, выделяемая во внешней цепи, достигает своего максимального значения, равного

. (6)

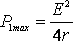
Когда источник замкнут на внешнее сопротивление, то ток протекает и внутри источника и при этом на внутреннем сопротивлении источника выделяется некоторое количество тепла. Мощность, затрачиваемая на выделение этого тепла равна

. (7)

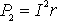
Следовательно, полная мощность, выделяемая во всей цепи , определится формулой

= I 2 (R+r) = IE (8)

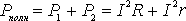
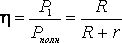
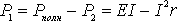
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ источника тока равен . (9)

, (10)

т.е. Р₁ изменяется с изменением силы тока в цепи по параболическому закону и принимает нулевые значения при I = 0 и при 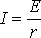. Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R Будет полезно почитать по теме:

источник

Мощность — это физическая величина, которую использует как основную характеристику любого устройства, которое применяют для совершения работы. Полезная мощность может быть использована для выполнения поставленной задачи.

Отношение работы ($\Delta A$) к промежутку времени за которое она выполнена ($\Delta t$) называют средней мощностью ($\left\langle P\right\rangle $) за это время:

\[\left\langle P\right\rangle =\frac\left(1\right).\]

Мгновенной мощностью или чаще просто мощностью называют предел отношения (1) при $\Delta t\to 0$:

\[\Delta A=\overline\cdot \Delta \overline\left(3\right),\]

где $\Delta \overline$ — перемещение тела под действием силы $\overline$, в выражении (2) имеем:

где $\ \overline-$ мгновенная скорость.

При выполнении необходимой (полезной) работы, например, механической, приходится выполнять работу большую по величине, так как в реальности существуют силы сопротивления и часть энергии подвержена диссипации (рассеиванию). Эффективность совершения работы определяется при помощи коэффициента полезного действия ($\eta $), при этом:

где $P_p$ — полезная мощность; $P$ — затраченная мощность. Из выражения (5) следует, что полезная мощность может быть найдена как:

Пусть электрическая цепь состоит из источника тока, имеющего сопротивление $r$ и нагрузки (сопротивление $R$). Мощность источника найдем как:

где $?$ — ЭДС источника тока; $I$ — сила тока. При этом $P$ — полная мощность цепи.

Обозначим $U$ — напряжение на внешнем участке цепи, тогда формулу (7) представим в виде:

где $P_p=UI=I^2R=\frac(9)$ — полезная мощность; $P_0=I^2r$ — мощность потерь. При этом КПД источника определяют как:

Максимальную полезную мощность (мощность на нагрузке) электрический ток дает, если внешнее сопротивление цепи будет равно внутреннему сопротивлению источника тока. При этом условии полезная мощность равна 50\% общей мощности.

При коротком замыкании (когда $R\to 0;;U\to 0$) или в режиме холостого хода $(R\to \infty ;;I\to 0$) полезная мощность равна нулю.

Задание. Коэффициент полезного действия электрического двигателя равен $\eta $ =42%. Какой будет его полезная мощность, если при напряжении $U=$110 В через двигатель идет ток силой $I=$10 А?

Решение. За основу решения задачи примем формулу:

Полную мощность найдем, используя выражение:

Подставляя правую часть выражения (1.2) в (1.1) находим, что:

Вычислим искомую мощность:

\[P_p=\eta IU=0,42\cdot 110\cdot 10=462\ \left(Вт\right).\]

Ответ. $P_p=462$ Вт

Задание. Какова максимальная полезная мощность источника тока, если ток короткого замыкания его равен $I_k$? При соединении с источником тока сопротивления $R$, по цепи (рис.1) идет ток силой $I$.

Решение. По закону Ома для цепи с источником тока мы имеем:

где $\varepsilon$ — ЭДС источника тока; $r$ — его внутреннее сопротивление.

При коротком замыкании считаем, что сопротивление внешней нагрузки равно нулю ($R=0$), тогда сила тока короткого замыкания равна:

Максимальная полезная мощность в цепи рис.1 электрический ток даст, при условии:

Тогда сила тока в цепи равна:

Максимальную полезную мощность найдем, используя формулу:

Мы получили систему из трех уравнений с тремя неизвестными:

Используя первое и второе уравнения системы (2.6) найдем $I’$:

Используем уравнения (2.1) и (2.2) выразим внутреннее сопротивление источника тока:

\[\varepsilon=I\left(R+r\right);;\ I_kr=\varepsilon \to I\left(R+r\right)=I_kr\to r\left(I_k+I\right)=IR\to r=\frac\left(2.8\right).\]

Подставим результаты из (2.7) и (2.8) в третью формулу системы (2.6), искомая мощность будет равна:

источник

В Московском государственном университете имени Ломоносова осуществляется проект по созданию демонстраторов 50-кубитных квантовых компьютеров к 2021 году. Основой для них послужат нейтральные атомы и интегральные оптические схемы. Над чем сейчас работают ученые?

В начале этого года по данной программе был успешно выполнен контрольный эксперимент по созданию ловушек для массивов нейтральных холодных атомов. Он проводился на базе лаборатории квантовых оптических технологий физического факультета МГУ. В будущем квантовом компьютере в этих ловушках будут фиксироваться атомы, находящиеся в состоянии хаотического движения. В квантовых компьютерах такие атомы являются носителями информации.
Стоит заметить, что квантовые компьютеры в отличие от классических вычислительных машин оперируют не битами, а кубитами, которые могут находится не только в состояниях «1» и «0», но и их суперпозиции. При разработке квантовых вычислительных устройств ученые стараются ввести кубиты в состояние квантовой запутанности. Суть явления заключается в том, что изменение одного кубита всегда влияет на состояние связанных с ним соседей. Благодаря этому квантовые компьютеры потенциально способны демонстрировать высокую производительность в вычислениях.
Важной вехой для квантовых технологий считается достижение так называемого квантового превосходства (то есть способности производить вычисления быстрее классических систем). Главной проблемой на текущем этапе развития квантовых технологий является возникновение в процессе работы большого количество ошибок, нуждающихся в коррекции, — сообщают российские исследователи.

Мощность, развиваемая источником тока во всей цепи, называется полной мощностью.

Она определяется по формуле

где P_об-полная мощность, развиваемая источником тока во всей цепи, вт;

В общем виде электрическая цепь состоит из внешнего участка (нагрузки) с сопротивлением R и внутреннего участка с сопротивлением R (сопротивлением источника тока).

Заменяя в выражении полной мощности величину э. д. с. через напряжения на участках цепи, получим

Величина UI соответствует мощности, развиваемой на внешнем участке цепи (нагрузке), и называется полезной мощностью P_пол=UI.

Величина U_oI соответствует мощности, бесполезно расходуемой внутри источника, Ее называют мощностью потерь P_o=U_oI.

Таким образом, полная мощность равна сумме полезной мощности и мощности потерь P_об=P_пол+P_0.

Отношение полезной мощности к полной мощности, развиваемой источником, называется коэффициентом полезного действия, сокращенно к. п. д.,и обозначается η.

При любых условиях коэффициент полезного действия η ≤ 1.

Если выразить мощности через величину тока и сопротивления участков цепи, получим

Таким образом, к. п. д. зависит от соотношения между внутренним сопротивлением источника и сопротивлением потребителя.

Обычно электрический к. п. д. принято выражать в процентах.

Для практической электротехники особый интерес представляют два вопроса:

1. Условие получения наибольшей полезной мощности

2. Условие получения наибольшего к. п. д.

Наибольшую полезную мощность( мощность на нагрузке) электрический ток развивает в том случае, если сопротивление нагрузки равно сопротивлению источника тока.

Эта наибольшая мощность равна половине всей мощности (50%) развиваемой источником тока во всей цепи.

Половина мощности развивается на нагрузке и половина развивается на внутреннем сопротивлении источника тока.

Если будем уменьшать сопротивление нагрузки, то мощность развиваемая на нагрузке будет уменьшаться а мощность развиваемая на внутреннем сопротивлении источника тока будет увеличиваться.

Если сопротивление нагрузки равно нулю то ток в цепи будет максимальным, это режим короткого замыкания (КЗ). Почти вся мощность будет развивается на внутреннем сопротивлении источника тока. Этот режим опасен для источника тока а также для всей цепи.

Если сопротивление нагрузки будем увеличивать, то ток в цепи будет уменьшатся, мощность на нагрузке также будет уменьшатся. При очень большом сопротивлении нагрузки тока в цепи вообще не будет. Это сопротивление называется бесконечно большим. Если цепь разомкнута то ее сопротивление бесконечно большое. Такой режим называется режимом холостого хода.

Таким образом, в режимах, близких к короткому замыканию и к холостому ходу, полезная мощность мала в первом случае за счет малой величины напряжения, а во втором за счет малой величины тока.

Коэффициент полезного действия (к. п. д.) равен 100% при холостом ходе ( в этом случае полезная мощность не выделяется, но в то же время и не затрачивается мощность источника).

По мере увеличения тока нагрузки к. п. д. уменьшается по прямолинейному закону.

В режиме короткого замыкания к. п. д. равен нулю ( полезной мощности нет, а мощность развиваемая источником, полностью расходуется внутри него).

Подводя итоги вышеизложенному, можно сделать выводы.

Условие получения максимальной полезной мощности( R=R) и условие получения максимального к. п. д. (R=∞) не совпадают. Более того, при получении от источника максимальной полезной мощности ( режим согласованной нагрузки) к. п. д.составляет 50%, т.е. половина развиваемой источником мощности бесполезно затрачивается внутри него.

В мощных электрических установках режим согласованной нагрузки является неприемлемым, так как при этом происходит бесполезная затрата больших мощностей. Поэтому для электрических станций и подстанций режимы работы генераторов, трансформаторов, выпрямителей рассчитываются так, чтобы обеспечивался высокий к. п. д. ( 90% и более).

Иначе обстоит дело в технике слабых токов. Возьмем, например, телефонный аппарат. При разговоре перед микрофоном в схеме аппарата создается электрический сигнал мощностью около 2 мвт. Очевидно, что для получения наибольшей дальности связи необходимо передать в линию как можно большую мощность, а для этого требуется выполнить режим согласованного включения нагрузки. Имеет ли в данном случае существенное значение к. п. д.? Конечно нет, так как потери энергии исчисляются долями или единицами милливатт.

Режим согласованной нагрузки применяется в радиоаппаратуре. В том случае, когда согласованный режим при непосредственном соединении генератора и нагрузки не обеспечивается, применяют меры согласования их сопротивлений.

источник

Рассмотрим замкнутую неразветвленную цепь, состоящую из источника тока и резистора.

Применим закон сохранения энергии ко всей цепи:

.

Так как , а для замкнутой цепи точки 1 и 2 совпадают, мощность электрических сил в замкнутой цепи равна нулю. Это равносильно утверждению о потенциальности электрического поля постоянного тока, о которой уже упоминалось ранее.

Итак, в замкнутой цепи всё тепло выделяется за счет работы сторонних сил: , или , и мы снова приходим к закону Ома, теперь для замкнутой цепи: .

Полной мощностью цепи называют мощность сторонних сил, она же равна полной тепловой мощности:

(1).

Полезнойназывают тепловую мощность, выделяемую во внешней цепи (независимо от того, полезна она или вредна в данном конкретном случае):

(2).

(3).

Роль электрических сил в цепи. Во внешней цепи, на нагрузке R, электрические силы совершают положительную работу, а при перемещении заряда внутри источника тока – такую же по величине отрицательную. Во внешней цепи теплота выделяется за счет работы электрического поля. Работу, отданную во внешней цепи, электрическое поле «возвращает» себе внутри источника тока. В итоге вся теплота в цепи «оплачена» работой сторонних сил: источник тока постепенно теряет запасенную в нем химическую (или какую-то другую) энергию. Электрическое же поле играет роль «курьера», доставляющего энергию во внешнюю цепь.

Зависимость полной, полезной мощностей и КПД от сопротивления нагрузки R.

Эти зависимости получаем из формул (1 – 2) и закона Ома для полной цепи:

. (4)

. (5)

Графики этих зависимостей вы видите на рисунке.

Полная мощность монотонно убывает с ростом , т.к. убывает сила тока в цепи. Максимальная полная мощностьвыделяется при , т.е. при коротком замыкании. Источник тока совершает максимальную работу за единицу времени, но вся она идет на нагревание самого источника. Максимальная полная мощность равна

.

Полезная мощность имеет максимум при (в чем вы можете убедиться, взяв производную от функции (5) и приравняв ее нулю). Подставив в выражение (5 ) , найдем максимальную полезную мощность:

.

Легко убедиться, что при полная мощность вдвое больше полезной.

На графике зависимости КПД от видно, что максимум КПД достигается при , однако при этом абсолютная величина полезной мощности стремится к нулю.

Дата добавления: 2015-06-12 ; просмотров: 11943 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

источник

При подключении электроприборов к электросети обычно имеет значение только мощность и КПД самого электроприбора. Но при использовании источника тока в замкнутой цепи важна полезная мощность, которую он выдаёт. В качестве источника могут применяться генератор, аккумулятор, батарея или элементы солнечной электростанции. Для расчётов это принципиального значения не имеет.

Замкнутая электрическая цепь

При подключении электроприборов к электропитанию и создании замкнутой цепи, кроме энергии Р, потребляемой нагрузкой, учитываются следующие параметры:

• Роб. (полная мощность источника тока), выделяемая на всех участках цепи;
• ЭДС – напряжение, вырабатываемое элементом питания;
• Р (полезная мощность), потребляемая всеми участками сети, кроме источника тока;
• Ро (мощность потерь), потраченная внутри батареи или генератора;
• внутреннее сопротивление элемента питания;
• КПД источника электропитания.

Внимание! Не следует путать КПД источника и нагрузки. При высоком коэффициенте батареи в электроприборе он может быть низким из-за потерь в проводах или самом устройстве, а также наоборот.

При прохождении электрического тока по цепи выделяется тепло, или совершается другая работа. Аккумулятор или генератор не являются исключением. Энергия, выделенная на всех элементах, включая провода, называется полной. Она рассчитывается по формуле Роб.=Ро.+Рпол., где:

• Роб. – полная мощность;
• Ро. – внутренние потери;
• Рпол. – полезная мощность.

Полная и полезная мощность

Внимание! Понятие о полной мощности используется не только в расчётах полной цепи, но также в расчетах электродвигателей и других устройств, потребляющих вместе с активной реактивную энергию.

ЭДС, или электродвижущая сила, – напряжение, вырабатываемое источником. Измерить его можно только в режиме Х.Х. (холостого хода). При подключении нагрузки и появлении тока от значения ЭДС вычитается Uо. – потери напряжения внутри питающего устройства.

Полезной называют энергию, выделенную во всей цепи, кроме питающего устройства. Она высчитывается по формуле:

1. «U» – напряжение на клеммах,
2. «I» – ток в цепи.

В ситуации, при которой сопротивление нагрузки равно сопротивлению источника тока, она максимальна и равна 50% полной.

При уменьшении сопротивления нагрузки ток в цепи растёт вместе с внутренними потерями, а напряжение продолжает падать, и при достижении нуля ток будет максимальным и ограниченным только Rо. Это режим К.З. – короткого замыкания. При этом энергия потерь равна полной.

При росте сопротивления нагрузки ток и внутренние потери падают, а напряжение растёт. При достижении бесконечно большой величины (разрыве сети) и I=0 напряжение будет равно ЭДС. Это режим Х..Х. – холостого хода.

Аккумуляторы, генераторы и другие устройства имеют внутреннее сопротивление. При протекании через них тока выделяется энергия потерь. Она рассчитывается по формуле:

где «Uо» – падение напряжения внутри прибора или разница между ЭДС и выходным напряжением.

Для расчёта потерь Ро. необходимо знать внутреннее сопротивление устройства. Это сопротивление обмоток генератора, электролита в аккумуляторе или по другим причинам. Замерить его мультиметром не всегда возможно. Приходится пользоваться косвенными методами:

• при включении прибора в режиме холостого хода замеряется Е (ЭДС);
• при подключенной нагрузке определяются Uвых. (выходное напряжение) и ток I;
• рассчитывается падение напряжения внутри устройства:

• вычисляется внутреннее сопротивление:

В зависимости от конкретных задач, необходима максимальная полезная мощность Р или максимум КПД. Условия для этого не совпадают:

• Р максимальна при R=Ro, при этом КПД = 50%;
• КПД 100% в режиме Х.Х., при этом Р=0.

Максимум Р достигается при условии равенства сопротивлений R (нагрузки) и Ro (источника электроэнергии). В этом случае КПД = 50%. Это режим «согласованной нагрузки».

Кроме него возможны два варианта:

• Сопротивление R падает, ток в цепи увеличивается, при этом растут потери напряжения Uo и Ро внутри устройства. В режиме К.З. (короткого замыкания) сопротивление нагрузки равно «0», I и Ро максимальны, а КПД также 0%. Этот режим опасен для аккумуляторов и генераторов, поэтому не используется. Исключение составляют практически вышедшие из употребления сварочные генераторы и автомобильные аккумуляторы, которые при запуске двигателя и включении стартёра работают в режиме, близком к «К.З.»;
• Сопротивление нагрузки больше внутреннего. В этом случае ток и мощность нагрузки Р падают, и при бесконечно большом сопротивлении они равны «0». Это режим Х.Х. (холостого хода). Внутренние потери в режиме, близком к Х.Х., очень малы, и КПД близок к 100%.

Следовательно, «Р» максимальна при равенстве внутреннего и внешнего сопротивлений и минимальна в остальных случаях за счёт высоких внутренних потерь при К.З и малого тока в режиме Х.Х.

Режим максимальной полезной мощности при эффективности 50% применяется в электронике при слабых токах. Например, в телефонном аппарате Рвых. микрофона – 2 милливатта, и важно максимально передать её в сеть, жертвуя при этом КПД.

Максимальная эффективность достигается в режиме Х.Х. за счёт отсутствия потерь мощности внутри источника напряжения Ро. При росте тока нагрузки КПД линейно уменьшается и в режиме К.З. равен «0». Режим максимальной эффективности используется в генераторах электростанций, где согласованная нагрузка, максимальная полезная Ро и КПД 50% неприменимы из-за больших потерь, составляющих половину всей энергии.

Эффективность электроприборов не зависит от батареи и никогда не достигает 100%. Исключение составляют кондиционеры и холодильники, работающие по принципу теплового насоса: охлаждение одного радиатора происходит за счёт нагрева другого. Если не учесть этот момент, то КПД получается выше 100%.

Энергия расходуется не только на выполнение полезной работы, но и на нагрев проводов, трение и другие виды потерь. В светильниках, кроме КПД самой лампы, следует обратить внимание на конструкцию отражателя, в нагревателях воздуха – на эффективность нагрева помещения, а в электродвигателях – на cos φ.

Знание полезной мощности элемента электропитания необходимо для выполнения расчётов. Без этого невозможно достичь максимальной эффективности работы всей системы.

источник

(12.10)

(12.11)

Коротким замыканием называется режим работы цепи, при котором внешнее сопротивление R = 0. При этом

(12.12)

(12.13)

График зависимости Р_а(I) – парабола, ветви которой направлены вниз (рис12.1). На этом же рисунке показаны зависимость КПД  от силы тока.

Задача 1. Батарея состоит из n = 5 последовательно соединённых элементов с Е = 1,4 В и внутренним сопротивлением r = 0,3 Ом каждый. При каком токе полезная мощность батареи равна 8 Вт? Какова наибольшая полезная мощность батареи?

Дано: Решение

n = 5 При последовательном соединении элементов ток в цепи

Е = 1,4 В (1)

Р_а = 8 Вт Из формулы полезной мощности выразим

внешнее сопротивление R и подставим в формулу (1)

I — ? -?

после преобразований получим квадратное уравнение, решая которое, найдём значение токов:

А; I₂ = A.

Итак, при токах I₁ и I₂ полезная мощность одинакова. При анализе графика зависимости полезной мощности от тока видно, что при I₁ потери мощности меньше и КПД выше.

Полезная мощность максимальна при R = n r; R = 0,3 Ом.

Ответ: I₁ = 2 A; I₂ = A;P_amax =Вт.

Задача 2. Полезная мощность, выделяемая во внешней части цепи, достигает наибольшего значения 5 Вт при силе тока 5 А. Найти внутреннее сопротивление и ЭДС источника тока.

Дано: Решение

P_amax = 5 Вт Полезная мощность (1)

I = 5 A по закону Ома (2)

.полезная мощность максимальна при R = r, то из

r — ? Е — ? формулы (1) 0,2 Ом.

Из формулы (2) В.

Задача 3. От генератора, ЭДС которого равна 110В, требуется передать энергию на расстояние 2,5 км по двухпроводной линии. Потребляемая мощность равна 10 кВт. Найти минимальное сечение медных подводящих проводов, если потери мощности в сети не должны превышать 1 %.

Дано: Решение

Е = 110 В Сопротивление проводов

l = 510 3 м где  — удельное сопротивление меди; l – длина проводов;

 = 1,710 -8 Ом . м Потребляемая мощность P_a= I E, мощность, теряемая

S — ? ток одинаковый, то

откуда

м 2 .

Задача 4. Найти внутреннее сопротивление генератора, если известно, что мощность, выделяемая во внешней цепи, одинакова при двух значениях внешнего сопротивления R₁ = 5 Ом и R₂ = 0,2 Ом. Найти КПД генератора в каждом из этих случаев.

Дано: Решение

R₁ = 5 Ом для замкнутой цепи тогда.

r -?

Преобразуя полученное равенство, находим внутреннее сопротивление источника r:

Ом.

Коэффициентом полезного действия называется величина

,

где Р_а – мощность, выделяемая во внешней цепи; Р – полная мощность.

Ответ: r = 1 Ом; = 83 %;= 17 %.

Задача 5. ЭДС батареи Е = 16 В, внутреннее сопротивление r = 3 Ом. Найти сопротивление внешней цепи, если известно, что в ней выделяется мощность Р_а = 16 Вт. Определить КПД батареи.

Дано: Решение

Е = 16 В Мощность, выделяемая во внешней части цепи Р_а= I 2 R.

r = 3 Ом Силу тока найдём по закону Ома для замкнутой цепи:

Р_а = 16 Вт тогда или

— ? R — ? Подставляем числовые значения заданных величин в это квадратное уравнение и решаем его относительно R:

Ом; R₂ = 9 Ом.

Ответ: R₁ = 1 Ом; R₂ = 9 Ом;

Задача 6. Две электрические лампочки включены в сеть параллельно. Сопротивление первой лампочки 360 Ом, сопротивление второй 240 Ом. Какая из лампочек поглощает большую мощность? Во сколько раз?

Дано: Решение

R₁ = 360 Ом Мощность, выделяемая в лампочке,

— ? При параллельном соединении на лампочках будет одинаковое напряжение, поэтому сравнивать мощности лучше, преобразовав формулу (1) используя закон Ома тогда

При параллельном соединении лампочек большая мощность выделяется в лампочке с меньшим сопротивлением.

Ответ:

Задача 7. Два потребителя сопротивлениями R₁ = 2 Ом и R₂ = 4 Ом подключаются к сети постоянного тока первый раз параллельно, а второй – последовательно. В каком случае потребляется большая мощность от сети? Рассмотреть случай, когда R₁ = R₂.

Дано: Решение

R₁ = 2 Ом Потребляемая от сети мощность

R₂ = 4 Ом (1)

— ? где R – общее сопротивление потребителей; U – напряжение в сети. При параллельном соединении потребителей их общее сопротивление а при последовательномR = R₁ + R₂.

В первом случае, согласно формуле (1), потребляемая мощность а во второмоткуда

Таким образом, при параллельном подключении нагрузок потребляется большая мощность от сети, чем при последовательном.

При

Ответ:

Задача 8.. Нагреватель кипятильника состоит из четырёх секций, сопротивление каждой секции R = 1 Ом. Нагреватель питается от аккумуляторной батареи с Е = 8 В и внутренним сопротивлением r = 1 Ом. Как следует подключить элементы нагревателя, чтобы вода в кипятильнике нагрелась в максимально короткий срок? Каковы при этом полная мощность, расходуемая аккумулятором, и его КПД?

Мак симальную полезную мощность источник даёт в случае, если внешнее сопротивление R равно внутреннему r.

Следовательно, чтобы воданагрелась в максимально короткий срок, нужно секции включить так,

чтобы R = r. Это условие выполняется при смешанном соединении секций (рис.12.2.а,б).

Мощность, которую расходует аккумулятор, равна Р = I E. По закону Ома для замкнутой цепи тогда

Вычислим 32 Вт;

Задача 9*. Ток в проводнике сопротивлением R = 12 Ом равномерно убывает от I = 5 А до нуля в течение времени  = 10 с. Какое количество теплоты выделяется в проводнике за это время?

Решение

Так как сила тока в проводнике изменяется, то для подсчёта количества теплоты формулой Q = I 2 R t воспользоваться нельзя.

Возьмём дифференциал dQ = I 2 R dt, тогда В силу равномерности изменения тока можно записатьI = k t, где k – коэффициент пропорциональности.

Значение коэффициента пропорциональности k найдём из условия, что при  = 10 с ток I = 5 А, I = k, отсюда

Подставим числовые значения:

Дж.

источник

Полная мощность источника тока:

P полн = P полезн + P потерь ,

где P полезн — полезная мощность, P полезн = I 2 R ; P потерь — мощность потерь, P потерь = I 2 r ; I — сила тока в цепи; R — сопротивление нагрузки (внешней цепи); r — внутреннее сопротивление источника тока.

Полная мощность может быть рассчитана по одной из трех формул:

P полн = I 2 ( R + r ), P полн = ℰ 2 R + r , P полн = I ℰ,

где ℰ — электродвижущая сила (ЭДС) источника тока.

Полезная мощность — это мощность, которая выделяется во внешней цепи, т.е. на нагрузке (резисторе), и может быть использована для каких-то целей.

Полезная мощность может быть рассчитана по одной из трех формул:

P полезн = I 2 R , P полезн = U 2 R , P полезн = IU ,

где I — сила тока в цепи; U — напряжение на клеммах (зажимах) источника тока; R — сопротивление нагрузки (внешней цепи).

Мощность потерь — это мощность, которая выделяется в источнике тока, т.е. во внутренней цепи, и расходуется на процессы, имеющие место в самом источнике; для каких-то других целей мощность потерь не может быть использована.

Мощность потерь, как правило, рассчитывается по формуле

где I — сила тока в цепи; r — внутреннее сопротивление источника тока.

При коротком замыкании полезная мощность обращается в нуль

так как сопротивление нагрузки в случае короткого замыкания отсутствует: R = 0.

Полная мощность при коротком замыкании источника совпадает с мощностью потерь и вычисляется по формуле

где ℰ — электродвижущая сила (ЭДС) источника тока; r — внутреннее сопротивление источника тока.

Полезная мощность имеет максимальное значение в случае, когда сопротивление нагрузки R равно внутреннему сопротивлению r источника тока:

Максимальное значение полезной мощности:

где P полн — полная мощность источника тока; P полн = ℰ 2 / 2 r .

В явном виде формула для расчета максимальной полезной мощности выглядит следующим образом:

Для упрощения расчетов полезно помнить два момента:

• если при двух сопротивлениях нагрузки R 1 и R 2 в цепи выделяется одинаковая полезная мощность, то внутреннее сопротивление источника тока r связано с указанными сопротивлениями формулой

• если в цепи выделяется максимальная полезная мощность, то сила тока I * в цепи в два раза меньше силы тока короткого замыкания i :

Пример 15. При замыкании на сопротивление 5,0 Ом батарея элементов дает ток силой 2,0 А. Ток короткого замыкания батареи равен 12 А. Рассчитать наибольшую полезную мощность батареи.

Решение . Проанализируем условие задачи.

1. При подключении батареи к сопротивлению R 1 = 5,0 Ом в цепи течет ток силой I 1 = 2,0 А, как показано на рис. а , определяемый законом Ома для полной цепи:

где ℰ — ЭДС источника тока; r — внутреннее сопротивление источника тока.

2. При замыкании батареи накоротко в цепи течет ток короткого замыкания, как показано на рис. б . Сила тока короткого замыкания определяется формулой

где i — сила тока короткого замыкания, i = 12 А.

3. При подключении батареи к сопротивлению R 2 = r в цепи течет ток силой I 2 , как показано на рис. в , определяемый законом Ома для полной цепи:

в этом случае в цепи выделяется максимальная полезная мощность:

P полезн max = I 2 2 R 2 = I 2 2 r .

Таким образом, для расчета максимальной полезной мощности необходимо определить внутреннее сопротивление источника тока r и силу тока I 2 .

Для того чтобы найти силу тока I 2 , запишем систему уравнений:

и выполним деление уравнений:

Для того чтобы найти внутреннее сопротивление источника r , запишем систему уравнений:

и выполним деление уравнений:

r = I 1 R 1 i − I 1 = 2,0 ⋅ 5,0 12 − 2,0 = 1,0 Ом.

Рассчитаем максимальную полезную мощность:

P полезн max = I 2 2 r = 6,0 2 ⋅ 1,0 = 36 Вт.

Таким образом, максимальная полезная мощность батареи составляет 36 Вт.

источник

Активная мощность (P)

Другими словами активную мощность можно назвать: фактическая, настоящая, полезная, реальная мощность. В цепи постоянного тока мощность, питающая нагрузку постоянного тока, определяется как простое произведение напряжения на нагрузке и протекающего тока, то есть

потому что в цепи постоянного тока нет понятия фазового угла между током и напряжением. Другими словами, в цепи постоянного тока нет никакого коэффициента мощности.

Но при синусоидальных сигналах, то есть в цепях переменного тока, ситуация сложнее из-за наличия разности фаз между током и напряжением. Поэтому среднее значение мощности (активная мощность), которая в действительности питает нагрузку, определяется как:

В цепи переменного тока, если она чисто активная (резистивная), формула для мощности та же самая, что и для постоянного тока: P = U I.

Формулы для активной мощности

P = U I — в цепях постоянного тока

P = U I cosθ — в однофазных цепях переменного тока

P = √3 U_L I_L cosθ — в трёхфазных цепях переменного тока

Активная мощность = √ (Полная мощность 2 – Реактивная мощность 2 ) или

Реактивная мощность (Q)

Также её мощно было бы назвать бесполезной или безваттной мощностью.

Мощность, которая постоянно перетекает туда и обратно между источником и нагрузкой, известна как реактивная (Q).

Реактивной называется мощность, которая потребляется и затем возвращается нагрузкой из-за её реактивных свойств. Единицей измерения активной мощности является ватт, 1 Вт = 1 В х 1 А. Энергия реактивной мощности сначала накапливается, а затем высвобождается в виде магнитного поля или электрического поля в случае, соответственно, индуктивности или конденсатора.

Реактивная мощность определяется, как

и может быть положительной (+Ue) для индуктивной нагрузки и отрицательной (-Ue) для емкостной нагрузки.

Единицей измерения реактивной мощности является вольт-ампер реактивный (вар): 1 вар = 1 В х 1 А. Проще говоря, единица реактивной мощности определяет величину магнитного или электрического поля, произведённого 1 В х 1 А.

Реактивная мощность = √ (Полная мощность 2 – Активная мощность 2 )

Полная мощность (S)

Полная мощность – это произведение напряжения и тока при игнорировании фазового угла между ними. Вся мощность в сети переменного тока (рассеиваемая и поглощаемая/возвращаемая) является полной.

Комбинация реактивной и активной мощностей называется полной мощностью. Произведение действующего значения напряжения на действующее значение тока в цепи переменного тока называется полной мощностью.

Она является произведением значений напряжения и тока без учёта фазового угла. Единицей измерения полной мощности (S) является ВА, 1 ВА = 1 В х 1 А. Если цепь чисто активная, полная мощность равна активной мощности, а в индуктивной или ёмкостной схеме (при наличии реактивного сопротивления) полная мощность больше активной мощности.

Полная мощность = √ (Активная мощность 2 + Реактивная мощность 2 )

• резистор потребляет активную мощность и отдаёт её в форме тепла и света.
• индуктивность потребляет реактивную мощность и отдаёт её в форме магнитного поля.
• конденсатор потребляет реактивную мощность и отдаёт её в форме электрического поля.

Все эти величины тригонометрически соотносятся друг с другом, как показано на рисунке:

источник

ИССЛЕДОВАНИЕ ПОЛЕЗНОЙ МОЩНОСТИ И КПД ИСТОЧНИКОВ ТОКА

Фамилия И.О. _____________ Группа ______ Дата ______

Цель данной работы – экспериментально проверить теоретические выводы о зависимости полезной мощности и КПД источника тока от сопротивления нагрузки.

Электрическая цепь состоит из источника тока, подводящих проводов и нагрузки или потребителя тока. Каждый из этих элементов цепи обладает сопротивлением.

Сопротивление подводящих проводов обычно бывает очень мало, поэтому им можно пренебречь. В каждом участке цепи будет расходоваться энергия источника тока. Весьма важное практическое значение имеет вопрос о целесообразном расходовании электрической энергии.

Полная мощность Р, выделяемая в цепи, будет слагаться из мощностей, выделяемых во внешней и внутренней частях цепи: P = I 2 ·R + I 2 ·r = I 2 (R + r). Так как I(R + r) = ε, то Р =I·ε,

где R – внешнее сопротивление; r – внутреннее сопротивление; ε – ЭДС источника тока.

Таким образом, полная мощность, выделяемая в цепи, выражается произведением силы тока на ЭДС элемента. Эта мощность выделяется за счет каких-либо сторонних источников энергии; такими источниками энергии могут быть, например, химические процессы, происходящие в элементе.

Рассмотрим, как зависит мощность, выделяемая в цепи, от внешнего сопротивления R, на которое замкнут элемент. Предположим, что элемент данной ЭДС и данного внутреннего сопротивления r замыкается внешним сопротивлением R; определим зависимость от R полной мощности Р, выделяемой в цепи, мощности Р_а, выделяемой во внешней части цепи и КПД.

Сила тока I в цепи выражается по закону Ома соотношением

Полная мощность, выделяемая в цепи, будет равна

При увеличении R мощность падает, стремясь асимптотически к нулю при неограниченном увеличении R.

Мощность, выделяющаяся во внешней части цепи, равна

Отсюда видно, что полезная мощность Р_а равна нулю в двух случаях – при R = 0 и R = ∞.

Исследуя функцию Р_а = f(R) на экстремум, получим, что Р_а достигает максимума при R = r, тогда

Чтобы убедится в том, что максимум мощности Р_а получается при R = r, возьмем производную Р_а по внешнему сопротивлению

По условию максимума требуется равенство нулю первой производной

r 2 = R 2

R = r

Можно убедиться, что при этом условии мы получим максимум, а не минимум для Р_а, определив знак второй производной .

Коэффициент полезного действия (КПД) η источника ЭДС это величина отношения мощности Р_а, выделяющейся во внешней цепи, к полной мощности Р, развиваемой источником ЭДС.

В сущности КПД источника ЭДС указывает, какая доля работы сторонних сил преобразуется в электрическую энергию и отдается во внешнюю цепь.

Выражая мощность через силу тока I, разность потенциалов во внешней цепи U и величину электродвижущей силы ε, получим

То есть КПД источника ЭДС равен отношению напряжения во внешней цепи к ЭДС. В условиях применимости закона Ома можно далее заменить U = IR; ε = I(R + r), тогда

Следовательно, в том случае, когда вся энергия расходуется на Ленц-Джоулево тепло, КПД источника ЭДС равен отношению внешнего сопротивления к полному сопротивлению цепи.

При R = 0 имеем η = 0. С увеличением R, КПД возрастает, стремится к значению η=1 при неограниченном увеличении R, однако при этом мощность, выделяющаяся во внешней цепи, стремится к нулю. Таким образом, требования одновременного получения максимальной полезной мощности при максимальном КПД невыполнимы.

Когда Р_а достигает максимума, то η = 50%. Когда же КПД η близок к единице, полезная мощность мала по сравнению с максимальной мощностью, которую мог бы развивать данный источник. Поэтому для увеличения КПД необходимо по возможности уменьшать внутреннее сопротивление источника ЭДС, например, аккумулятора или динамо-машины.

В случае R = 0 (короткое замыкание) Р_а = 0 и вся мощность выделяется внутри источника. Это может привести к перегреву внутренних частей источника и выводу его из строя. По этой причине короткие замыкания источников (динамо-машины, аккумуляторные батареи) недопустимы!

На рис. 1 кривая 1 дает зависимость мощности Р_а, выделяемой во внешней цепи, от сопротивления внешней части цепи R; кривая 2 дает зависимость от R полной мощности Р; кривая 3 – ход КПД η от того же внешнего сопротивления.

Порядок выполнения работы

1. Ознакомиться со схемой на стенде.

2. Установить с помощью магазина сопротивление R = 100 Ом.

4. Произвести измерения силы тока в цепи последовательно для различных девяти сопротивлений на магазине сопротивлений, начиная от 100 Ом и выше. Внести в таблицу результаты измерений силы тока, выразив их в амперах.

6. Вычислить для каждого сопротивления Р, Р_а (в ваттах) и η.

7. Построить графики Р, Р_а и η от R.

1. Что называется КПД источника ЭДС?

2. Вывести формулу КПД источника ЭДС.

3. Что такое полезная мощность источника ЭДС?

4. Вывести формулу полезной мощности источника ЭДС.

5. Чему равна максимальная мощность, выделяемая во внешней цепи (Ра)max?

6. При каком значении R полная мощность Р, выделяющаяся в цепи, максимальна?

7. Чему равен КПД источника ЭДС при (Ра)max?

8. Произвести исследование функции (Ра) = f(R) на экстремум.

9. Зарисовать график зависимости Р, Ра и η от внешнего сопротивления R.

10. Что такое ЭДС источника?

11. Почему сторонние силы должны быть не электрического происхождения?

12. Почему недопустимо короткое замыкание для источников напряжения?

, Вт

, Вт

источник

В электротехнике среди множества определений довольно часто используются такие понятия, как активная, реактивная и полная мощность. Эти параметры напрямую связаны с током и напряжением в замкнутой электрической цепи, когда включены какие-либо потребители. Для проведения вычислений применяются различные формулы, среди которых основной является произведение напряжения и силы тока. Прежде всего это касается постоянного напряжения. Однако в цепях переменного тока мощность разделяется на несколько составляющих, отмеченных выше. Вычисление каждой из них также осуществляется с помощью формул, благодаря которым можно получить точные результаты.

Основной составляющей считается активная мощность. Она представляет собой величину, характеризующую процесс преобразования электрической энергии в другие виды энергии. То есть по-другому является скоростью, с какой потребляется электроэнергия. Именно это значение отображается на электросчетчике и оплачивается потребителями. Вычисление активной мощности выполняется по формуле: P = U x I x cosф.

В отличие от активной, которая относится к той энергии, которая непосредственно потребляется электроприборами и преобразуется в другие виды энергии – тепловую, световую, механическую и т.д., реактивная мощность является своеобразным невидимым помощником. С ее участием создаются электромагнитные поля, потребляемые электродвигателями. Прежде всего она определяет характер нагрузки, и может не только генерироваться, но и потребляться. Расчеты реактивной мощности производятся по формуле: Q = U x I x sinф.

Полной мощностью является величина, состоящая из активной и реактивной составляющих. Именно она обеспечивает потребителям необходимое количество электроэнергии и поддерживает их в рабочем состоянии. Для ее расчетов применяется формула: S = .

Активная мощность относится к энергии, которая необратимо расходуется источником за единицу времени для выполнения потребителем какой-либо полезной работы. В процессе потребления, как уже было отмечено, она преобразуется в другие виды энергии.

В цепи переменного тока значение активной мощности определяется, как средний показатель мгновенной мощности за установленный период времени. Следовательно, среднее значение за этот период будет зависеть от угла сдвига фаз между током и напряжением и не будет равной нулю, при условии присутствия на данном участке цепи активного сопротивления. Последний фактор и определяет название активной мощности. Именно через активное сопротивление электроэнергия необратимо преобразуется в другие виды энергии.

При выполнении расчетов электрических цепей широко используется понятие реактивной мощности. С ее участием происходят такие процессы, как обмен энергией между источниками и реактивными элементами цепи. Данный параметр численно будет равен амплитуде, которой обладает переменная составляющая мгновенной мощности цепи.

Существует определенная зависимость реактивной мощности от знака угла ф, отображенного на рисунке. В связи с этим, она будет иметь положительное или отрицательное значение. В отличие от активной мощности, измеряемой в ваттах, реактивная мощность измеряется в вар – вольт-амперах реактивных. Итоговое значение реактивной мощности в разветвленных электрических цепях представляет собой алгебраическую сумму таких же мощностей у каждого элемента цепи с учетом их индивидуальных характеристик.

Основной составляющей полной мощности является максимально возможная активная мощность при заранее известных токе и напряжении. При этом, cosф равен 1, когда отсутствует сдвиг фаз между током и напряжением. В состав полной мощности входит и реактивная составляющая, что хорошо видно из формулы, представленной выше. Единицей измерения данного параметра служит вольт-ампер (ВА).

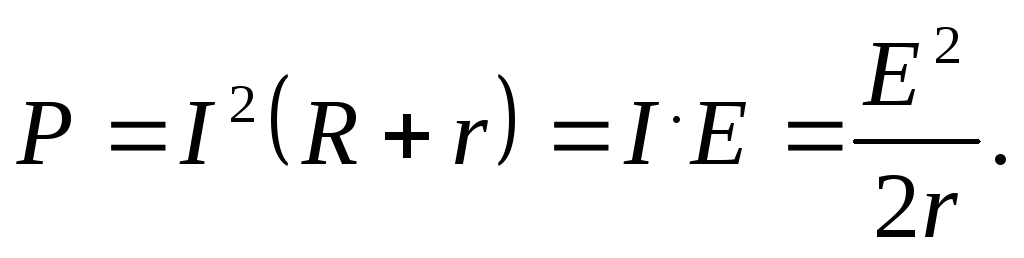
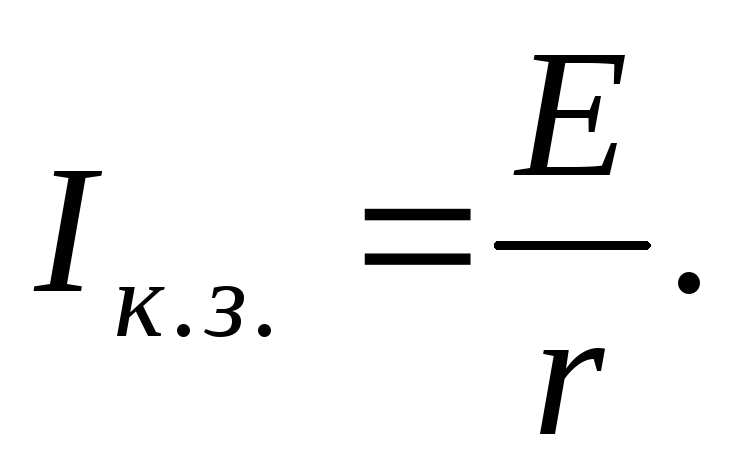
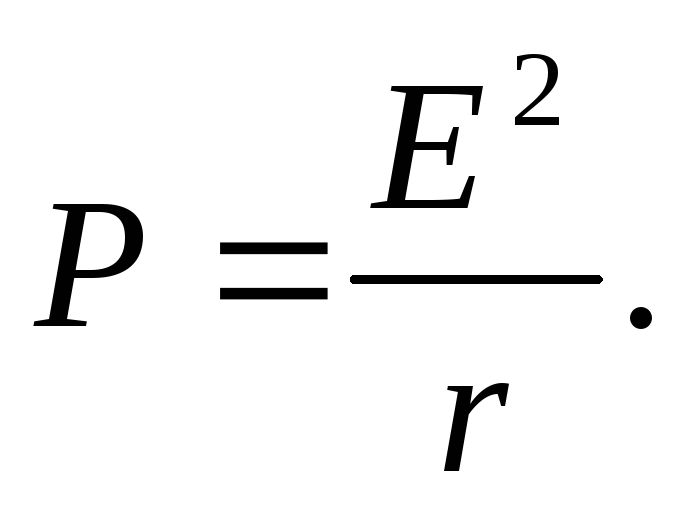
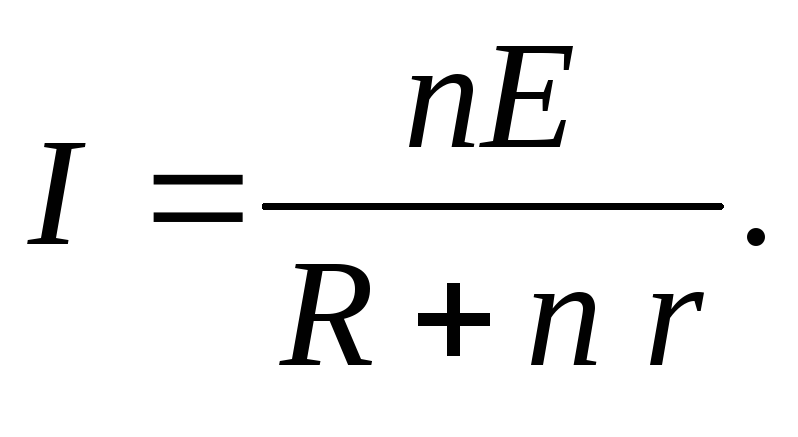
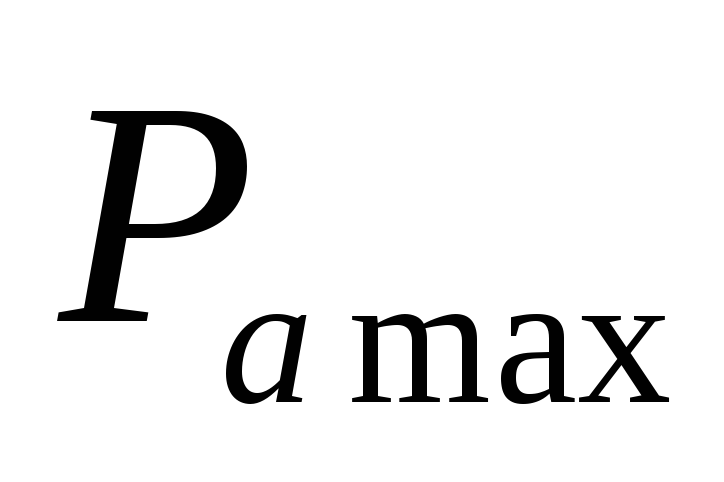
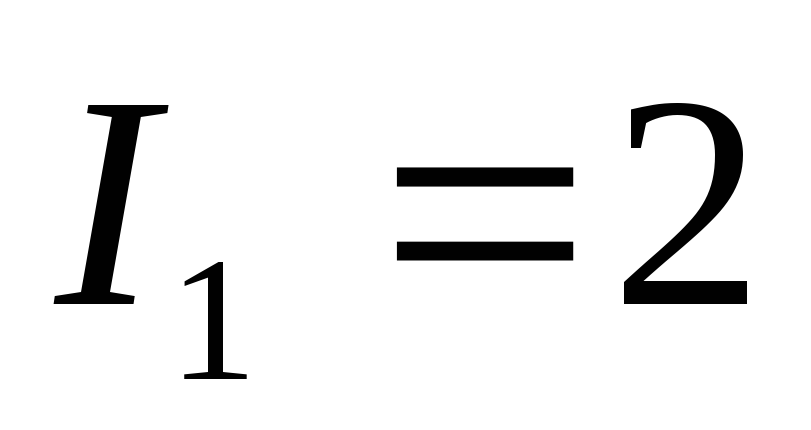
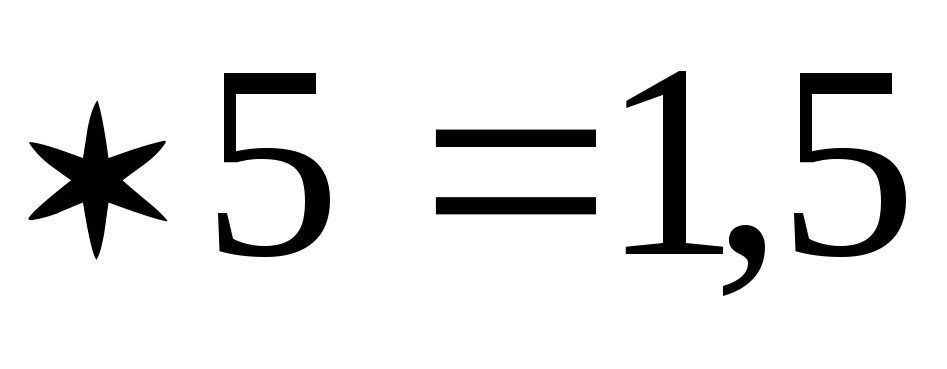
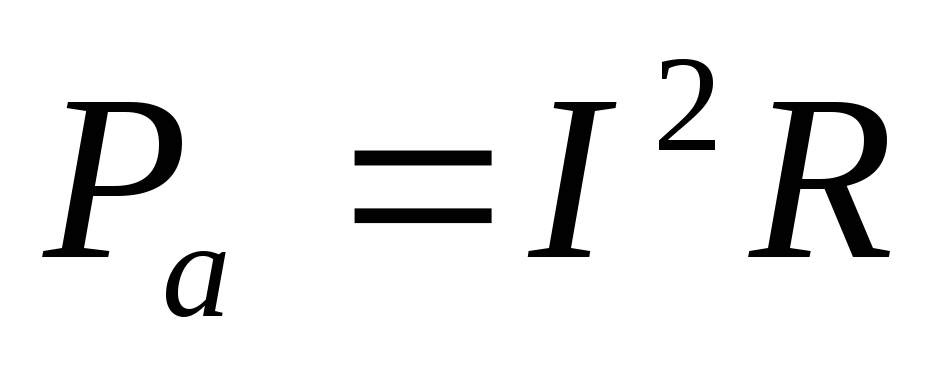
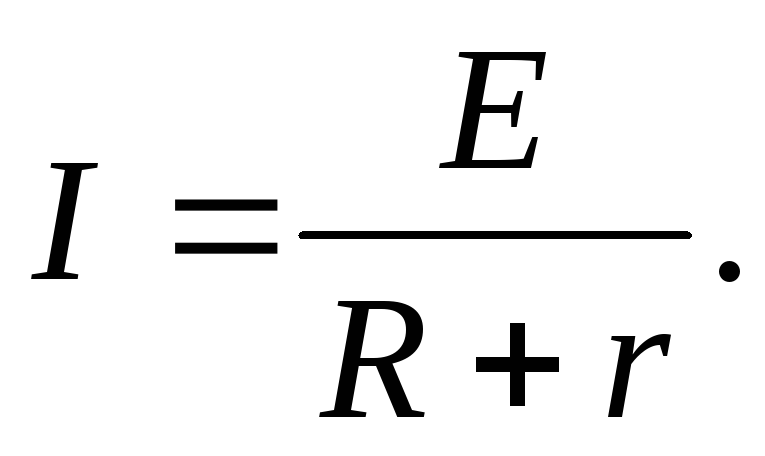
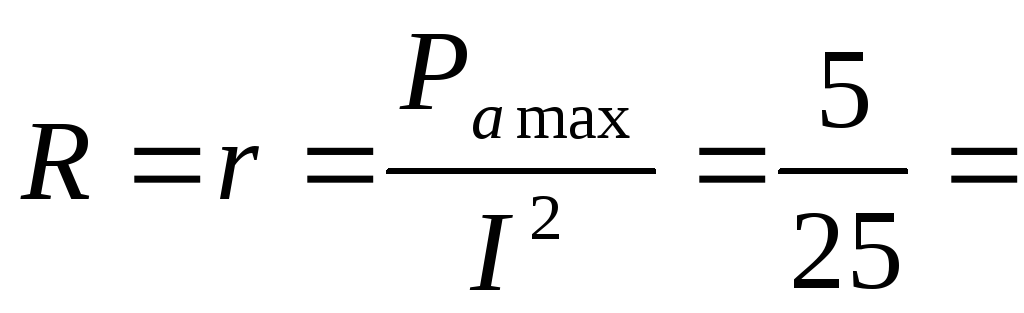
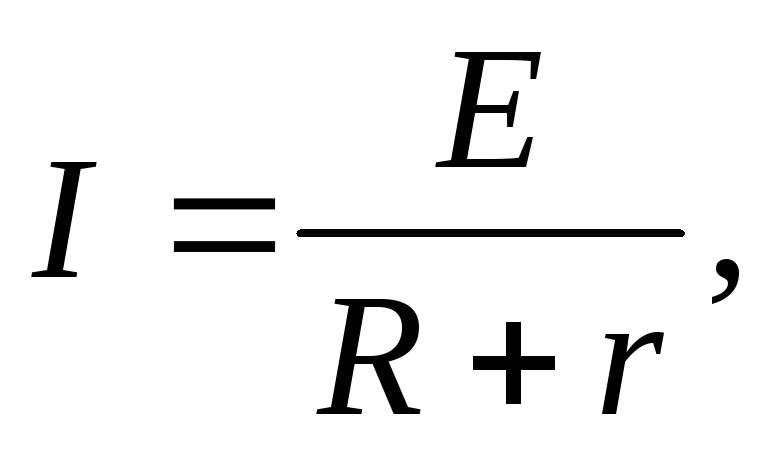
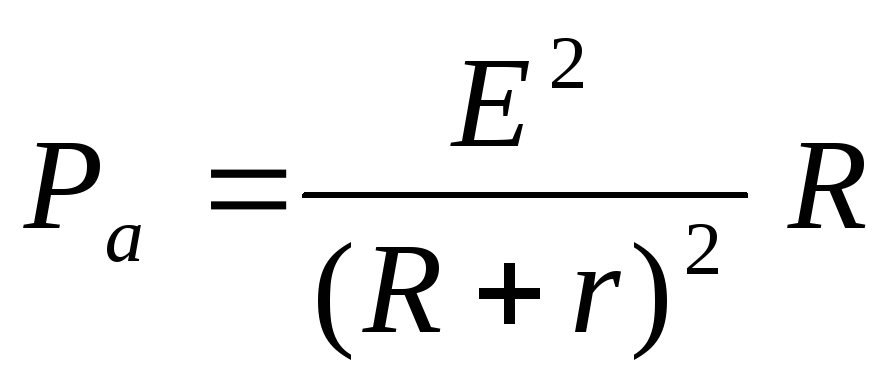
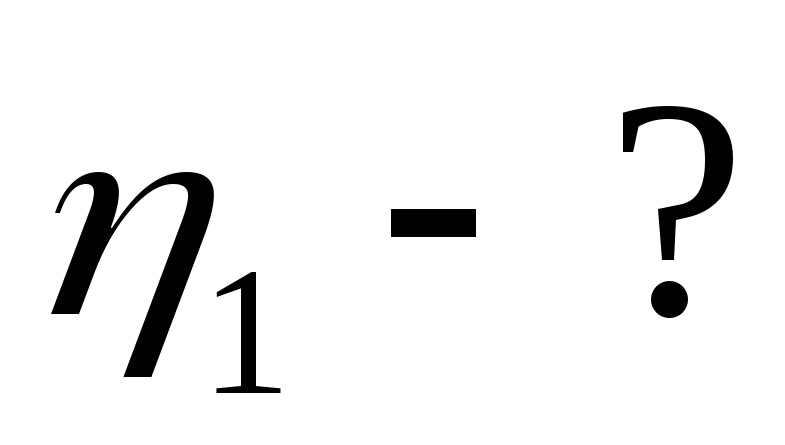
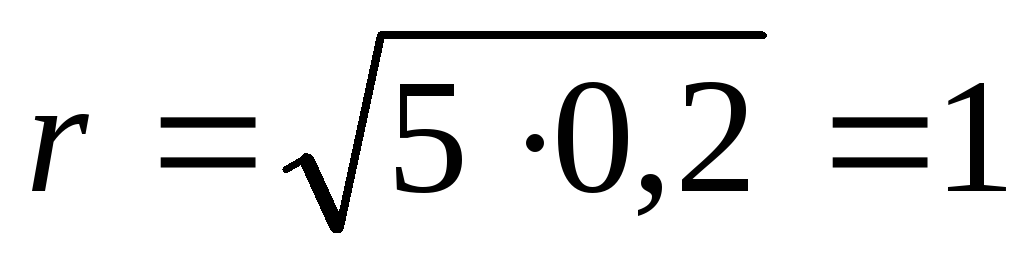
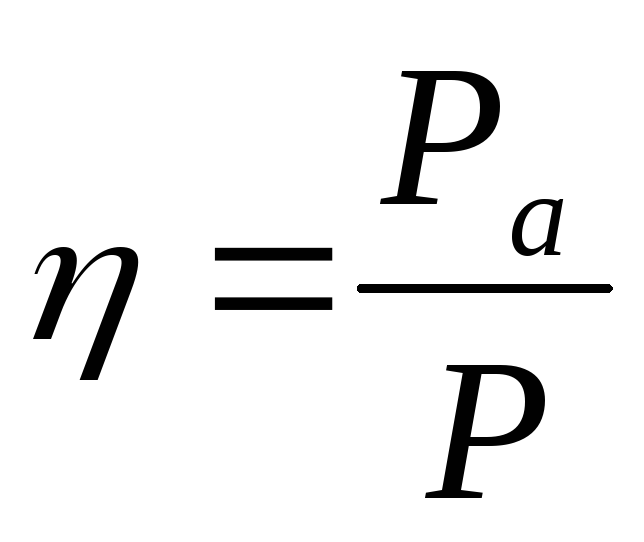
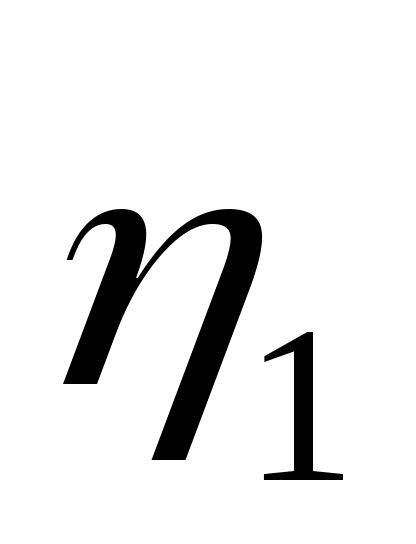
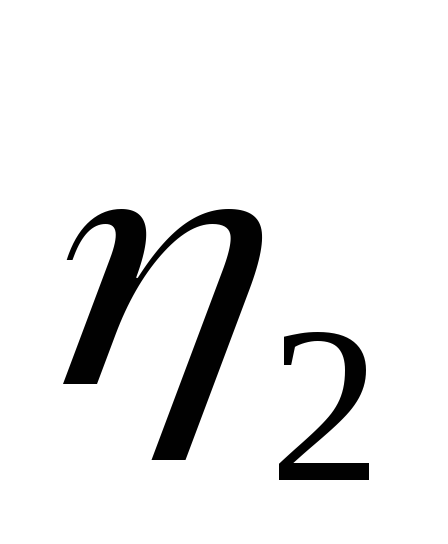
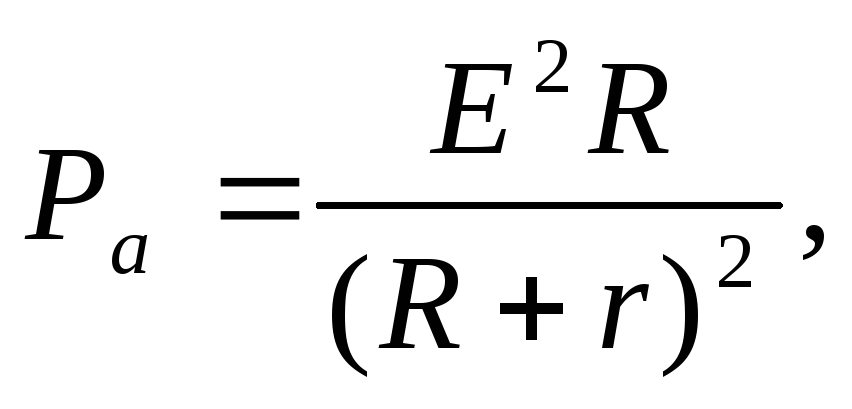
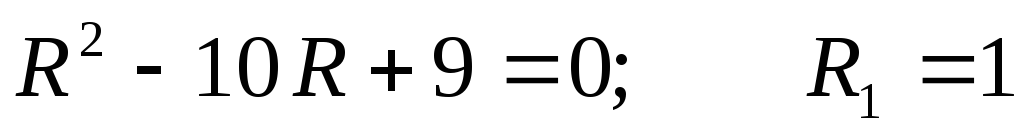
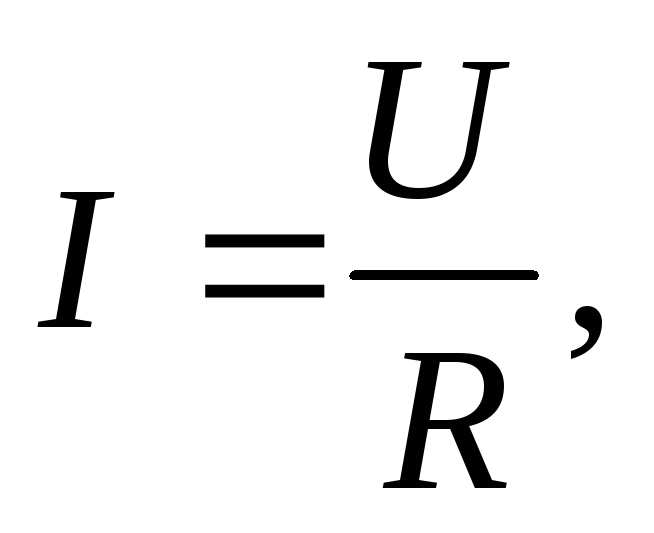
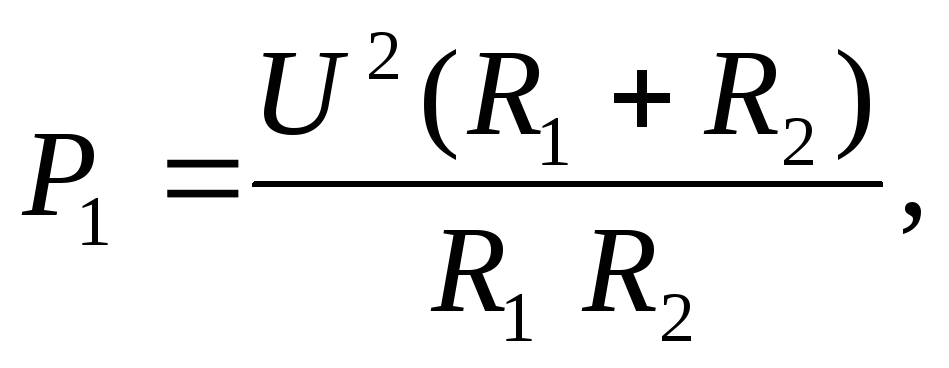
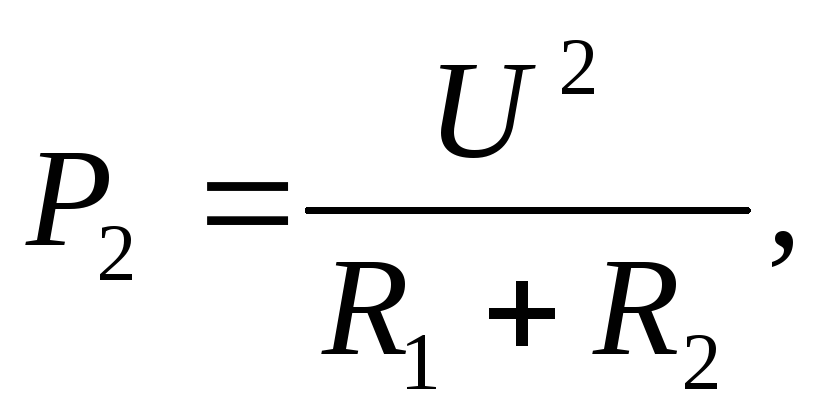
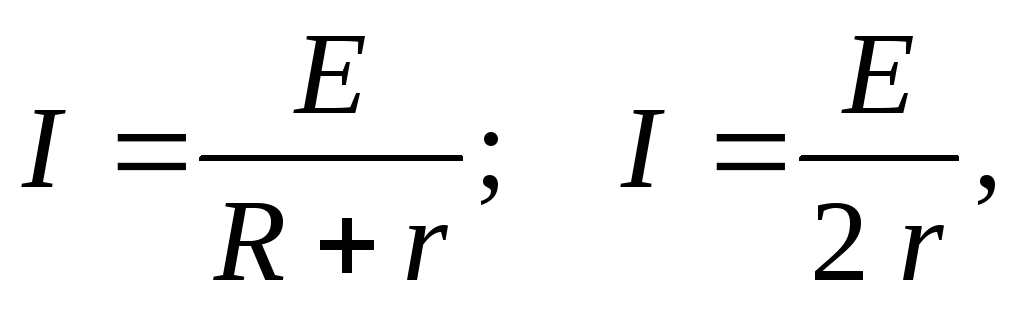
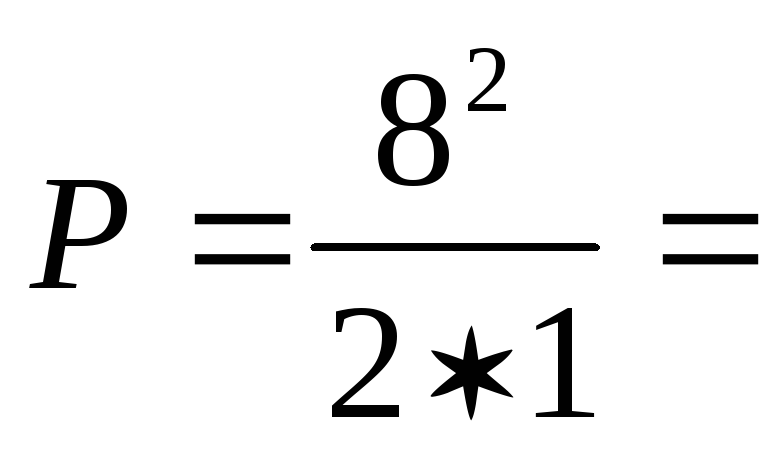
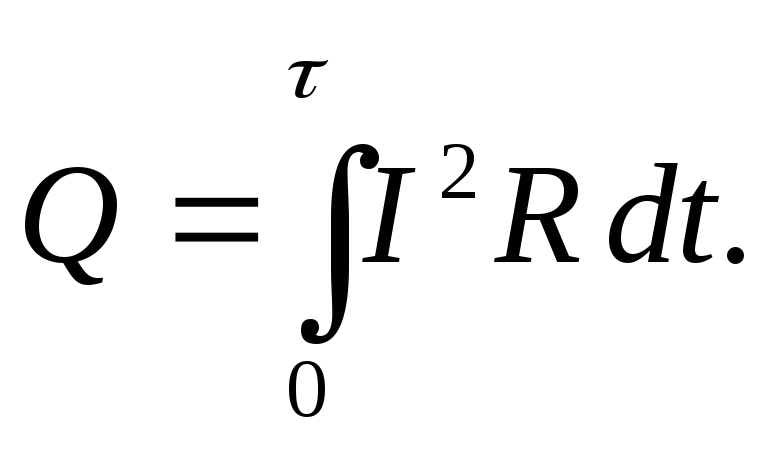
источник