Бинарные отношения и функция выбора не всегда удобны для моделирования экономических систем и анализа этих моделей. Гораздо чаще используется функция, которая в числовой форме выражает предпочтения лица, принимающего решение. В микроэкономике это понятие используется для объяснения поведения предпринимателей и потребителей, в макроэкономике предпочтения рассматриваются с точки зрения государственных интересов.
Вещественная функция u, определенная на множестве A и удовлетворяющая условиям
u () > u (), тогда и только тогда, когда P, (1.3.1)
для любых ,A , называется порядковой функцией полезности для отношения P на A. Если для отношение предпочтения P определена функция полезности u, то
u()=u(), тогда и только тогда, когда I.
Отсюда следует, что классами безразличия в A будут подмножества альтернатив c одинаковыми значениями функции u.
Функции u и v являются порядковыми функциями полезности для отношения P на A, несмотря на то, что в первом случае полезность альтернативы равна 999, а во втором — только 1.
Каким же условиям должно удовлетворять отношение предпочтения P, чтобы вместо него можно было рассматривать функцию полезности? Этот вопрос до сих пор является предметом дискуссий. Дело в том, что дополнительные требования к отношению предпочтения вводятся аксиоматически и обоснованность той или иной системы аксиом не является бесспорной.
Если множество A состоит из детерминированных исходов, то для существования функции полезности достаточно выполнения аксиом 1- 6. Однако, эксперт (инвестор, ЛПР), поставленный перед проблемой выбора, не всегда с полной определенностью знает последствия этого выбора. Например, полезность покупки может оказаться меньше (или больше) ожидаемой из-за изменений условий ее использования. Кроме того, результаты некоторых действий всегда имеют случайный характер (ситуации с элементами риска). Рисковые ситуации часто возникают в банковской сфере, на финансовых рынках, в инновационной и предпринимательской деятельности промышленных предприятий и т.д. Дж. фон Нейман и О.Моргенштерн предположили, что потребитель в случайных ситуациях ведет себя рационально, то есть из многочисленных альтернатив он выбирает ту, которая дает наибольшую ожидаемую полезность. Вероятности возможных исходов должны быть известны.
Простой лотереей (или лотереей) L=(p,x;(1- p),y) называется случайное событие с двумя возможными исходами x и y, вероятности которых равны p и (1-p), 0? p?1. На рис.1.3.1.(a) дана графическая иллюстрация случайного события z, являющегося лотереей L=(p,x;(1- p),y). Аналогично определяется лотерея с тремя и большим числом возможных исходов. Теория полезности предполагает, что для каждой пары лотерей лицо, принимающее решение, может определить, какая лотерея для него предпочтительней (лучше). Отношения предпочтения на множестве лотерей аналогичны бинарным отношениям R, P и I на множестве альтернатив A. Детерминированное событие можно рассматривать как частный случай лотереи.
Рис.1.3.1. Лотерея с двумя исходами
Для измерения ожидаемой полезности уже не достаточно выбирать шкалы, согласованные друг с другом только в отношении порядка.
Пример 1.3.2. Пусть A= и P, P, P. Рассмотрим две порядковые функции полезности для отношения P на A
Сравним теперь промежуточную альтернативу с лотерей L=(,;,), состоящей в случайном выборе между наилучшей альтернативой и наихудшей альтернативой . Получаем:
источник
Функция полезности потребителя описывается формулой U = XY/2, где X – объём потребления бананов, Y – объём потребления пепси-колы. Цена 1 кг бананов 3$, 1 л пепси-колы – 2$, летом потребитель тратил на эти товары 20$ в неделю. Зимой цена бананов поднялась до 5$ за килограмм, цена пепси-колы не изменилась. Определите:
1) Объём оптимального потребления бананов и пепси-колы летом.
2) Величину расходов, необходимую зимой для достижения того же уровня полезности, что и летом.
3) Количественное значение эффекта дохода и эффекта замены.
Решение. Бюджетные возможности можно представить в виде равенства: M = PXX + PY Y, где:
X и Y – количество товаров, приобретаемых потребителем;
Бюджетные возможности потребителя при покупке бананов (товар X) и пепси-колы (товар Y) летом можно выразить формулой 3X + 2Y = 20.
На основе этой формулы надо построить бюджетную линию. Наклон бюджетной линии определяется обратным соотношением цен и характеризует пропорцию замены или соотношение товаров X и Y в наборе:
NЗ= = , или = . По условию задачи = .
Равновесие потребителя достигается в точке касания бюджетной линии с графиком безразличия, где их углы наклона совпадают, а значит, соотношение товаров в наборе на графике безразличия должно соответствовать соотношению товаров на бюджетной линии и определяться соотношением цен. Иными словами для графика безразличия в точке касания MRSxy=∆Y/ ∆X = PX / PY.
Или, также как для бюджетной линии, соотношение товаров в наборе равно = .;
Соотношение товаров в наборе определяется соотношением цен, а количество товара X и товара Y зависит от величины дохода.
1. Для определения оптимального набора составим и решим систему уравнений:
3X + 3X = 20, отсюда X = 3,3; соответственно Y = 5.
Оптимальное потребление составит 3,3 кг бананов и 5 л пепси-колы.
Определим величину общей полезности данного набора:
U = XY/2 = (3,3 . 5)/2 → U = 8,25.
Эта полезность соответствует всем наборам, находящимся на графике безразличия, который можно вывести из формулы полезности U = XY/2 и выразить функцией Y = 2U/X → Y = 16,5/X
2.Определим набор, соответствующий такому же уровню полезности, но при более высокой цене товара X.
Соотношение товаров в наборе изменится в связи с увеличением цены бананов (товар X): = .
Количество товара X и товара Y должно быть таким, чтобы при изменившемся соотношении общая полезность набора не изменилась, то есть новый набор должен находится на существующем графике безразличия. Составим и решим новую систему уравнений с учетом функции полезности:
1. = → Y = 5X/2
16,5 = (5X/2) . X
16,5 = 5X 2 /2 → 33 = 5X 2 → X 2 = 6,7 → X = 2,6; Y = X . 5/2 = 6,5.
Набор 2,6 кг бананов и 6,5 л пепси-колы соответствует такому же уровню полезности, что и в первом наборе. Согласно свойствам графика безразличия уменьшение одного блага сопровождалось увеличением другого в такой пропорции, что общая полезность оставалось постоянной величиной.
Определим бюджет потребителя, соответствующий новому равновесному набору, исходя из формулы бюджетных возможностей:
M = 5 . 2,6 + 2 . 6,5 = 26$, то есть доход потребителя должен возрасти.
3. Эффект замещения составит (3,3 кг – 2,6 кг) = – 0,7 кг бананов и (6,5 кг – 5 кг) = + 1,5 пепси-колы.
Эффект дохода. Если бы покупатель тратил зимой на покупки 20$, то его оптимальный набор при новом соотношении цен составил бы 2 кг бананов и 5 л пепси-колы. Это можно определить, составив систему уравнений (см. п. 1).
2. =
Отсюда Y = 5/2 . X → 5X + 2(5/2 . X) = 20 →
5X + 5X = 20, отсюда X = 2; соответственно Y = 5.
Следовательно, эффект дохода составляет 0,6 кг бананов (2,6 кг – 2 кг) 1,5 л пепси-колы (6,5 л – 5 л).
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10044 — 

193.124.117.139 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
источник
1. В каком отношении распределится налоговое бремя между потребителем и производителем, если 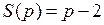
2. Для функции полезности 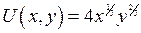
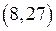
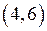
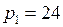
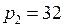
3. Приведение задачи линейного программирования к каноническому виду.
4. Приведение задачи линейного программирования к стандартному виду.
5. Составление двойственной задачи линейного программирования.
6. Решение задачи линейного программирования методом перебора вершин допустимого множества.
7. Решение задачи линейного программирования графическим методом.
8. Решение задачи линейного программирования симплекс-методом.
9. Решение задачи линейного программирования методом искусственного базиса.
10. Решение транспортной задачи. Построение опорного плана методом наименьшего тарифа. Улучшение плана методом потенциалов.
11. Для заданной транспортной задачи 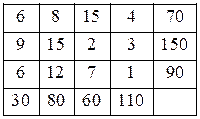
12. Пусть запасы поставщиков равны 60, 130 и 90 (закрытая модель), от 
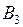
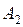
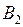
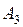
Текущий контроль осуществляется в ходе учебного процесса и контроля самостоятельной работы студентов, а также по результатам выполнения домашней контрольной работы. Основными формами текущего контроля знаний являются:
· решение задач, входящих в план практических занятий;
· обсуждение вопросов и методов решений задач с экономическими приложениями;
· выполнение контрольных заданий и обсуждение результатов.
Промежуточная аттестация проводится в первом семестре в форме письменного экзамена в виде решений задач и ответа на теоретические вопросы экзаменационного билета.
Оценка знаний студентов осуществляется в баллах с учетом оценки работы в семестре (выполнение контрольной работы, аудиторных самостоятельных работ и домашних заданий, решение задач и участие в обсуждениях на практических занятиях и др.), оценки итоговых знаний (по результатам экзамена) и в соответствии с критериями Финансового университета реализуется следующим образом:
| № п/п | Вид отчетности | Баллы |
| 1. | Работа в семестре | |
| 2. | Зачет (экзамен) | |
| Итого: |
Формы текущего контроля успеваемости и их балльная оценка
Аттестация 1 (середина семестра)
| № | Формы текущего контроля | Количество баллов за половину семестра |
| 1. | Активное участие в семинарах | |
| 2. | Выполнение домашних заданий | |
| 3. | Контрольная работа и самостоятельные аудиторные работы | |
| Итого |
Дата добавления: 2017-03-12 ; просмотров: 217 | Нарушение авторских прав
источник
1 Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» (Финансовый университет) Кафедра «Прикладная математика» И.А. Александрова, В.М. Гончаренко МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ Руководство к решению задач Учебное пособие для подготовки бакалавров Одобрено кафедрой «Прикладная математика», протокол 7 от февраля г. Москва
2 УДК ББК Рецензенты: В.В. Киселев, доцент, к. ф.-.м. н. (Финуниверситет) И.Б. Тесленко, д.э.н. (Владимирский Государственный университет) Александрова И.А., Гончаренко В.М. Методы оптимальных решений. Руководство к решению задач: учебное пособие для подготовки бакалавров. М.: Финуниверситет,. с. ISBN В пособии рассматриваются различные методы оптимизации, кокоторые применяются для решения прикладных задач экономики и финансов. Последовательно рассматриваются различные виды функций, возникающих в экономических задачах и их свойства, варианты постановки и методы решения транспортной задачи, методы решения задач целочисленного программирования и многокритериальной оптимизации, элементы теории игр и методы динамического и выпуклого программирования. Изложение сопровождается различными примерами задач, возникающих из практики, и составлено в полном соответствии с программой дисциплины «Методы оптимальных решений», входящей в базовую часть математического цикла ФГОС по направлению «Экономика» подготовки бакалавров. В каждом параграфе имеются задачи для самостоятельного решения, все они снабжены ответами. По каждой теме приводится краткий перечень основных теоретических положений, разбираются наиболее важные примеры, определяющих основные требования к знаниям и умениям студентов. Пособие предназначено для подготовки бакалавров экономики и менеджемента Финакадемии. Оно может быть использовано как для проведения семинарских занятий, так и для организации самостоятельной работы студентов. УДК ББК ISBN И.А. Александрова, В.М. Гончаренко, Финуниверситет,
3 Содержание Введение. 5 Глава. ВВЕДЕНИЕ В МЕТОДЫ ОПТИМИЗАЦИИ. 6.. Функция спроса и ее эластичность. 6.. Функция предложения и рыночное равновесие Предельные величины в экономике и оптимизация прибыли. Основные виды функций нескольких переменных в экономических задачах Предельная полезность товара и предельная норма замещения Критерий оптимального набора товаров и оптимального производственного плана Глава. ТРАНСПОРТНАЯ ЗАДАЧА.. Постановка задачи.. Построение начального опорного плана транспортной задачи 5.. Решение транспортной задачи методом потенциалов 9.. Открытая модель транспортной задачи. 5. Определение оптимального плана транспортных задач с дополнительными ограничениями. 6 Глава. МЕТОД ИСКУССТВЕННОГО БАЗИСА.. Симплекс-метод решения задач линейного программирования.. Метод искусственного базиса. 7 Глава. ЗАДАЧИ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ. 5.. Постановка задачи. Графический метод решения 5.. Двойственный симплекс-метод Метод Гомори 6 Глава 5. ЗАДАЧИ МНОГОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ Общая постановка задачи многокритериальной оптимизации. Парето-эффективное множество. 65Ошибка! Закладка не определена. 5.. Методы решения многокритериальной задачи оптимизации 7 Глава 6. ЭЛЕМЕНТЫ ТЕОРИИ ИГР Платежная матрица. Нижняя и верхняя цена игры Решение игры в смешанных стратегиях Приведение матричной игры к задаче линейного программирования Игра с природой 86 Глава 7. ВЫПУКЛЫЕ ФУНКЦИИ И ТЕОРЕМА КУНА-ТАККЕРА 9
4 7.. Выпуклые функции Теорема Куна-Таккера.. 9 Глава 8. МЕТОДЫ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 8.. Задача динамического программирования 8.. Задача о распределении средств между предприятиями. Рекомендуемая литература
5 Введение Пособие предназначено для подготовки бакалавров и написано в соответствии с двумя основными целями. Первая из них состоит в том, чтобы продемонстрировать, как основные знания, полученные при изучении базовых дисциплин «Математический анализ», «Линейная алгебра» и «Теория вероятностей и математическая статистика» применяются для решения экономических задач, возникающих на практике. Второй основной целью данного пособия является формирование навыков по составлению математических моделей различных задач оптимизации, возникающих в экономике, и применению многообразия математических методов для их решения. Последовательно рассматриваются различные виды функций, возникающих в экономических задачах и их свойства, варианты постановки и методы решения транспортной задачи, методы решения задач целочисленного программирования и многокритериальной оптимизации, элементы теории игр и методы динамического и выпуклого программирования. Изложение сопровождается различными примерами задач, возникающих из практики, и составлено в полном соответствии с программой дисциплины «Методы оптимальных решений», входящей в базовую часть математического цикла ФГОС по направлению «Экономика» подготовки бакалавров. Главы 5, 6 написаны И.А. Александровой, а главы -, 7-8 В.М. Гончаренко. Один из авторов (В.М. Гончаренко) хотел бы выразить свою признательность студенту -ого курса факультета «Математические методы и анализ рисков» Д. Щуровскому за указания и исправления опечаток в методических пособия [5], материалы которого стали основой некоторых глав этой книги. 5
6 Глава Введение в методы оптимизации Целью данной главы является напоминание основных фактов из базового курса математического анализа, которые необходимы для понимания приложений математических методов для решения экономических задач. Функция спроса и ее эластичность В этом параграфе мы подробно остановимся на функции спроса и экономическом смысле понятия эластичности. Функция спроса Dp (demd) определяет спрос (количество купленного товара) при цене p за единицу продукции. Понятие эластичности было введено Аланом Маршаллом в связи с изучением D p. свойств функции 6 Определение.. Эластичностью относительное изменение спроса p p цены товара: D D E D спроса Dp называется при относительном изменении D % E D D (.) p % p Если функция спроса является дифференцируемой, то под эластичностью понимается предел правой части формулы (.) при p. Тогда эластичность E D спроса вычисляется по формуле D ED pl D p. (.) D Заметим, что (.) вполне согласуется с используемой в математическом анализе формуле для эластичности произвольной дифференцируемой функции y
7 y Ey l y y Замечание.. В силу экономического смысла функция спроса D p и цена p принимают положительные значения. По той же при- чине Dp является невозрастающей функцией p. Поэтому производная D p E являются неположитель- и, в силу (.), эластичность D ными величинами. Определение.. Спрос называется эластичным, если ED, и неэластичным, если ED, Замечание.. Если функция спроса не зависит от цены, т.е. ED, то спрос называют совершенно неэластичным. Если же малое изменение цены приводит к значительному изменению спроса, то говорят, что спрос является совершенно эластичным, и полагают, что E. D Пример.. Пусть функция спроса D p Сp, C,. Найти эластичность спроса и значения параметра, при которых спрос эластичен. Решение. В силу ограничений на параметры C и функция Dp является положительной и убывающей. При этом C Cp D Cp и E D. Поэтому E D, и p p Cp спрос эластичен при и неэластичен при. Поясним теперь важность разделения эластичного и неэластичного спроса. Так как спрос D p является количеством проданного по цене p товара, то общая выручка (totl reveue) TR (или просто R ) R p D p. Поэтому равна R pd p pd p D pd, а эластичность выручки R D pd D pd D ER p p p ED. R pd D D Рассматривая случаи эластичного спроса, т.е. ED ( ED ) и неэластичного спроса ED ( E D ), приходим к следующему выводу: в первом случае ER, а во втором ER. Таким образом, При эластичном спросе изменение цены приводит к изменению выручки в противоположном направлении, т.е. увеличение (уменьшение) цены приводит к уменьшению (увеличению) выручки. Если же 7
8 спрос неэластичен, то изменение цены вызывает изменение выручки в том же направлении, т.е. увеличение (уменьшение) цены приводит к увеличению (уменьшению) выручки. 8 Пример.. Пусть функция спроса D p p. Исследовать зависимость между эластичностью спроса и доходом от продажи товара. Решение. Поскольку функция спроса равна количеству реали- q D p p, то общий доход R, получае- зованного товара, т.е. мый при спросе Dp, равен D p и p положительны, то будем рассматри- Так как величины вать функцию R p на промежутке R( p) p, то R p pd p p p p p. ;. При этом, так как R p возрастает при p 6 и убывает при 6 p. D p С другой стороны, ED p. В силу замечания. условие эластичности спроса ED можно переписать в виде ED. р D p Решая неравенство с учетом p, получаем p p 6,, т.е интервал, на котором функция R p убывает. Таким образом, при эластичном спросе цену товара повышать не выгодно. Аналогично, условие неэластичности спроса ED можно переписать в виде ED, т.е. p,6. Последний интервал совпадает с множеством, на котором доход R возрастает с увеличением цены. При неэластичном спросе увеличение цены товара приводит к увеличению выручки. Наряду с общей выручкой важной для приложений является функция издержек фирмы. Компания, как правило, имеет фиксированные издержки FC (fed cost), которые не зависят от объемов призведенной продукции, и переменные издержки VC (vrble cost). Общие издержки TC (totl cost) являются суммой TC FC VC, причем FC TC. Множество, на котором общие издержки равны общей выручке, т.е. TC TR, называется безубыточным множеством. Пример.. Пусть функция общих издержек ТС p 8p 6, а функция общей выручки равна TR 8p. Найти множество безубыточности.
9 Решение. Решая уравнение TC TR, т.е. p 8p6 8p, получим p и p 8. Таким образом, множество безубыточности состоит из двух точек. При этом легко видеть, что производство убыточно (TR TC ) при p,8, и прибыльно при остальных p. При подготовке задач для самостоятельного решения главы использованы материалы пособий [] и []. Задачи для самостоятельного решения. Найти эластичность спроса при цене p, если Dp8 p. Эластичен ли спрос при данной цене?. Исследовать зависимость между эластичностью спроса и доходом от продажи товара, если фукнция спроса D p 6 p.. Пусть функция общих издержек ТС p p 8, а функция общей выручки равна TR p. Найти множество безубыточности. При каких ценах производство убыточно. Функция предложения и рыночное равновесие Функция предложения (supply) S p задает количество товара, которое поставщик может предложить по рыночной цене p. В силу своего экономического смысла, функция предложения Sp является неотрицательной и неубывающей. Определение.. Говорят, что рынок находится в равновесии, если покупатели могут купить столько товара, сколько им необходимо, а продавец может реализовать весь товар, который он намерен продать. Равновесная цена p товара на рынке находится из условия Sp Dp, а количество q проданного товара q Dp. Пример.. Пусть функция спроса задана функцией D p p p, а функция предложения равна S p p p. Найти равновесную цену и количество проданного товара. Решение. Решая уравнение p p p p, получим, p p9, т.е. p 5 и p 6. 9
10 В силу экономического смысла задачи q D p 7 p имеем p 5, Пример.5 (задача о распределении налогового бремени). Найти изменение равновесной цены при введении дополнительного налога t на единицу продукции, если D p p, S( p) 7p. Как распределится бремя дополнительного налога между потребителем и производителем? Решение. Если на производителя вводится дополнительный налог в размере t (t) на каждую единицу продукции, то при новой равновесной цене товара p t стоимость единицы продукции для потребителя равна p t, а для производителя выручка с единицы продукции составляет pt t (t исключается из выручки как налоговая выплата). Поэтому p t находится из уравнения S( pt t) D( pt). Итак, из уравнения p 7 p 6 находим исходную равновесную цену 7 p t 6 p для новой p. Решая уравнение 7 7 равновесной цены p t, получим, что pt t p t. Таким образом, равновесная цена выросла по сравнению с p, но не на полную величину налога, а на ее часть: бремя налога делится между потребителем и производителем в отношении 7:. Если функции спроса и предложения заданы произвольными линейными функциями D p d d p, S( p) sp s, где d, d, s, s R, d, d, то легко показать, что бремя дополнительного налога разделится между потребителем и производителем в отношении s : d. 8,, p. Задачи для самостоятельного решения. Пусть функция кратковременного спроса имеет вид D p p и кратковременного предложения S p Найти эластичность кратковременного спроса в точке рыночного равновесия. t t
11 D p p p, 5. Пусть функция спроса задана функцией 5 а функция предложения равна 5 S p p p. Найти равновесную цену и количество проданного товара. 6. Найти изменение равновесной цены при введении дополнительного налога t на единицу продукции, если Dp p, S( p) 6p. Как распределится бремя дополнительного налога между потребителем и производителем. Предельные величины в экономике и оптимизация прибыли Наряду с функциями издержек, дохода и т.д. в экономике рассматриваются соответсвующие предельные величины. К ним относятся предельные издержки, предельный доход, предельная производительность, предельная полезность и т.д. Предельная величина определяется как отношение относительного изменения Y величи- Y X ны Y YX (например, дохода фирмы) при изменении X величины X (например, объема производства): Y MY. X Если же YX является дифференцируемой функцией, то предельную величину рассматривают при X : Y MY lm Y X. X Одной из задач оптимизации, естественно возникающих в микроэкономике, является задача об оптимизации прибыли. Необходимое условие максимизации прибыли формулируют как равенство предельного дохода предельным издержкам, т.е. MR MC. (.) Если функции выручки и издержек являются дифференцируемыми, то условие (.) можно записать в виде R( q) C( q). При этом, так как функция прибыли q равна разности функций дохода и издержек ( q) R( q) C( q), то необходимое условие экстремума ( q) записывается как R( q) C( q), что эквивлентно (.).
12 Пример.6. Пусть C q q q 7q 8 функция полных затрат на производство q единиц товара, Rq q q функция дохода от продажи. Найти максимум прибыли. Решение. Находим функцию прибыли ( q) R q C q q q 6q 8, ее производную ( q) 6q 66q 6 и критические точки: q и q (рис..). + Рис.. Таким образом, максимум прибыли достигается в точке q и m () 699. Заметим, что m () 98. Отрицательная прибыль при низком объеме выпуска товаров объясняется тем, что затраты на их производство больше выручки от продажи. Пример.7. Функция спроса q D p p, фиксированные издержки равны FC 5 и переменные издержки VC q,q. Найти максимальную прибыль, множество безубыточности, предельные издержки и доход. Решение. Общие издержки равны TC VC FC,q q 5. Далее, из условия q p находим, что p,q, и общая выручка TR = pq = q,q. Отсюда получаем формулу для прибыли q TRTC,q q 5. Легко прове- Из условия q получим,8q, т.е. q 5 рить, что эта точка является точкой максимума, и Решая уравнение q m 5 6., находим множество безубыточности, состоящее из двух точек q, 5 5 6, а предельные издержки и выручка получаются как производные общих выручки и издержек: MC TC,6q и MR TR’,q. Рассмотрим теперь задачу об оптимизации налогообложения. Предположим, что на продукцию компании вводится (дополнительный) фиксированный налог t на каждую единицу реализованного то-
13 вара. Если ставка налога достаточно велика, то производство товара будет невыгодно, и это приведет к его остановке. Естественно, возникает вопрос о такой ставке налога, чтобы итоговый сбор был максимальным. Пример.8 (оптимизация налогообложения). Пусть R( q) 5q q доход (выручка) от продажи, а Cq ( ) q 6q затраты на выпуск продукта в зависимости от количества q. Найти величину налога t на каждую единицу продукта, чтобы налог T tq от всей реализуемой продукции был максимальным, и весь налоговый сбор. Как уменьшится количество выпускаемой продукции? Решение. Найдем сначала объем производства без учета дополнительного налога. Так как q 5q 6q, то из условия qq6 находим, что максимум прибыли достигается при объеме производства q 6. Из-за введения дополнительного налога доход производителя ( T ) уменьшится на величину T и составит R ( q) 5qq tq, а его прибыль ( T ) q R q C q q qtq ( ) 5 6. В результате компания исходит из того, чтобы при реализации товара получить максимальную прибыль. Решая уравнение ( q), находим 6 qt, т.е. q 6 t/. Общая налоговая выплата будет составлять T tq6 t t /. Вычислим теперь максимум функции T Tt. Из условия T() t следует, что 6 t /5, т.е. t. Легко видеть, что точка t является точкой максимума функции Tt. () При этом весь налоговый сбор T 6 / 9 и объем производства равен q 6/. Таким образом, введение дополнительного налога уменьшает объем производства в два раза (с 6 до единиц продукции). 7. Пусть Задачи для самостоятельного решения 76 функция полных за- C q q q q трат на производство q единиц товара, Rq 5q q функция дохода от продажи. Найти максимум прибыли.
14 8. Функция спроса задана в виде p5,q, фиксированные издержки равны FC 5 и переменные издержки VC 6q,q. Найти максимальную прибыль, точку безубыточности, предельные издержки и доход. 9. Пусть Rq ( ) 66q q доход (выручка) от продажи, а Cq ( ) q 6q затраты на выпуск продукта в зависимости от количества q. Найти величину налога t на каждую единицу продукта, чтобы налог T tq от всей реализуемой продукции был максимальным, и весь налоговый сбор. Как уменьшится количество выпускаемой продукции. Основные виды функций нескольких переменных в экономических задачах Рассмотрим теперь основные виды функций нескольких переменных, которые встречаются в экономических задачах. Пусть X, X,, X ресурсы, используемые для производства, а. соответствующие количества. Определение.. Производственной функцией Q Q. называется функция, выражающая объем продукции Q, полученной при использовании ресурсов (факторов) X, X,, X в количествах. соответственно. Если, то Q называется однофакторной функцией, а при многофакторной. В силу экономического смысла переменные. и значения Q предполагаются неотрицательными. Различные виды производственных функций возникают в экономических задачах как функции, описывающие тот или иной производственный процесс и используются для анализа или прогноза деятельности компании, корпорации или отрасли. Так, двухфакторная производственная функция Кобба Дугласа QK, L K L, где,, (.) названа в честь американских ученых Чарльза Кобба и Пола Дугласа, которые в 98 году предприняли попытку эмпирическим путем определить влияние затрачиваемого капитала и труда на объем выпускаемой продукции в обрабатывающей промышленности США. Они установили, что зависимость объема производства от объема используемого капитала и трудовых ресурсов связаны соотношением (.).
15 Функцией Кобба-Дугласа иногда называют двухфакторную функцию вида более общего вида QK, L K L, (.5) где. Функции (.), (.5) являются частными случаями мультипликативных производственных функций вида Q. (.6) где. Наряду с мультипликативными производственными функциями рассматривают также линейные производственные функции вида Q. где. производственные функции Леонтьева. m. Q, (.7) где. и другие. Каждая этих производственных функций связана с тем или иным технологическим процессом. Определение.5. Геометрическое место точек в пространстве факторов, в которых различные сочетания факторов производства (ресурсов) дают одно и то же количество выпускаемой продукции называют изоквантой. В связи с понятием изокванты естественно возникает вопрос о возможности замещения одного из ресурсов другими при сохранении объемов производства. Так, если процесс описывается функцией Кобба-Дугласа (.), то из условия K L Q легко выразить как K, так и L через остальные параметры производства. Поэтому для любого положительного количества одного ресурса можно подобрать такое количество другого ресурса, что возможно произвести любой требуемый объем продукции. Наоборот, функция Леонтьева (.7) характеризует такой производственный процесс, при котором замена одного ресурса другими невозможна при любом объеме производства, и избыток одного ресурса не может компенсировать недостаток другого. Рассмотрим еще один пример. Двухфакторная линейная производственная функция, функции Леонтьева и Кобба-Дугласа являются частными или предельными случаями производственной функции CES (costt elstcty of substtuto) Q K, L F K L, (.8) / 5
16 где F,, некоторые параметры. Она была введена американским экономистом Нобелевским лауреатом Р.Солоу в 956 г. Оказывается, для изоквант функции (.8) для каждого из ресурсов существуют пороговые значения, такие, что если количество ресурсов меньше этих значений, то замещение одного из ресурсов другим невозможно. Подробнее о структуре изоквант для каждой из производственных функций (.), (.7), (.8) можно прочитать в пособии []. Определение.6. Функцией полезности (utlty fucto) U U. называется функция, описывающая предпочтения потребителей на множестве товаров X, X,, X и выражающая ценность набора товаров в количествах. соот- U. U y, y,, y для ветственно. При этом, если двух различных наборов и y y y y. то набор является более полезным для потребителя, чем набор y. Ясно, что у каждого потребителя имеются свои предпочтения, поэтому и функция полезности у каждого индивидуальна. При решении практических задач нередко рассматривают (усреднённую) функцию полезности, характерную для некоторой категории потребителей. Замечание.. Из определения.6 следует, что значение функции полезности на данном наборе товаров безразлично. Существенным является лишь то, как это значение соотносится со значениями функции полезности на прочих наборах товаров. Определение.7. Геометрическое место точек в пространстве товаров, в которых различные комбинации товаров дают одно и то же значение функции полезности U U. называют линией безразличия. Среди примеров функций полезности упомянем функцию U(, ) C, где C. и ее обощение. U, (.9) где, при. представляет собой минимально допустимый набор товаров. Ввиду замечания. в приложениях иногда удобнее рассматривать логарифмическую функцию полезности U l l l,. При этом 6
17 A O U, М U B Рис.. p p I где, при. которая получается логарифмированием функции (.9). Пусть теперь I денежная сумма, которую потребитель может потратить на приобретение товаров X, X,, X, а p k цена единицы товара X k, k. Тогда стоимость набора товаров. равна p p p, а бюджетное ограничение имеет вид p p p I. (.) Определение.8. Множество наборов товаров. стоимость которых удовлетворяет бюджетному ограничению (.), называется бюджетным множеством. Если при этом предпочтения потребителей характеризуются функцией полезности U U. и потребитель намерен употребить свои средства с наибольшей для себя пользой, то оптимальным набором товаров будет та точка из бюджетного множества, в которой функция полезности принимает наибольшее значение. Пример.9. Рассмотрим случай (см. рис..). Бюджетное множество (.) задает треугольник OAB, а оптимальный набор товаров задается точкой касания M его границы AB и кривой безразличия, наиболее удаленной от начала координат, как имеющей наибольшую полезность среди всех линий безразличия, имеющих общие точки с бюджетным множеством. Пример.. Для товаров X и X известны функции спроса q 5 p, q 5 p. Фирма-монополист имеет функцию издержек C q 6qq q. Вычислите максимальную прибыль фирмы в этих условиях и найдите соответствующий производственный план. Решение. Последовательно находим общую выручку 7
18 R q, q pq p q 5q q 7q q q q 5q 7q и прибыль q, q R q, q C q, q q 5q 5q 7q 6qq. Критические точки функции q, q находим из системы ‘ q 6q 6q 5, ‘ q 6q q 7, решением которой является точка 5,. Так как матрица вторых производных G функции q, q не зависит от точки и равна qq qq 6 6 G qq 6, qq то по критерию Сильвестра убеждаемся, что точка 5, является точкой максимума функции q, q и m 5, 7. Задачи для самостоятельного решения. Фирма-монополист продает товар на трех независимых рынках. Функции спроса на этих рынках линейны и имеют вид qp,5,6p, qp,65,8p, q p,5,5 p. Издержки на производство q единиц товара равны Cq55 9q. Определите цену на каждом из рынков, при которых фирма получит максимальную прибыль.. Фирма-монополист продает товар на двух независимых рынках. Функции спроса на этих рынках имеют вид q, p q. Издержки на производство q единиц товара равны p Cq q. Определите объемы продаж на каждом из рынков, при которых фирма получит максимальную прибыль.. Для товаров X и X известны функции спроса: q 5 p, q 75 p. Фирма-монополист имеет функцию издержек C q 5qq 6q 7. При каком производственном плане прибыль максимальна? 8
19 .5. Предельная полезность товара и предельная норма замещения Пусть U U. функция полезности, описывающая предпочтения потребителя (или некоторой категории потребителей) на множестве товаров X, X,, X. Аналогично п.. введем следующее определение. Определение.9. Предельной полезностью товара X k называется частная производная функции U U. по переменной k U k lm k U. Таким образом, предельная полезность товара равна X k скорости изменения полезности набора товаров M. при незначительном изменении его количества k. Ясно, что она приблизительно равна изменению полезности набора товаров M при изменении количества товара X U k на одну единицу: U k. При этом, так k как увеличение количества одного товара, как правило, приводит к повышению полезности набора, то, очевидно, что предельная полезность величина неотрицательная. Чтобы сохранить неизменной полезность набора, следует, увеличивая количество одного товара, одновременно уменьшать количество другого товара. Определение.. Предельной нормой замещения MRSX k, X l M (mgl rte of substtuto) товара X k товаром X l для набора M. называется отношение предельных полезностей товаров X k и X l : U M k MRSX, k X M. l U M Предельная норма замещения приблизительно равна количеству товара X l, которое может заменить единицу товара X k в исходном наборе M. так, чтобы полезность набора товаров не изменилась. Из определения естественно получаем, что k l 9
20 MRSX, k X M. l MRSX, l X M k Определение.. Изоклиной для пары товаров X k и X l называется множество наборов товаров M. для которых предельная норма замещения товара X k товаром X l постоянна MRSX, X M cost. k l Пример.. Вычислите предельную норму замещения ресурса X ресурсом X в точке (,8), если функции полезности Кобба / / Дугласа U, C, а также найдите уравнение изоклины, проходящей через эту точку. Решение. Найдем сначала предельные полезности ресурсов X и X : C / / C / / U, U, Тогда предельная норма замещения имеет вид C / / U 8 MRSX, X, MRS X, X,8 /. U C / / Таким образом, искомое уравнение изоклины имеет вид MRS X, X /, т.е. /, или, окончательно, 9. Задачи для самостоятельного решения. Вычислите предельную норму замещения ресурса X ресурсом X в точке, 8, если функции полезности Кобба Дугласа / / U, C, а также найдите уравнение изоклины, проходящей через эту точку.. Для функции полезности U, y f и набора товаров вычислите предельные полезности первого и второго товаров, а также предельную норму замещения MRS X, X первого товара вторым.
21 .6. Критерий оптимального набора товаров и оптимального производственного плана. Рассмотрим теперь несколько задач, непосредсвенно связанных с понятием предельной нормы замещения. Если известна функция полезности U U, потребителя (мы ограничимся случаем ), то вполне естетсвенно поставить вопрос о выборе оптимального набора товаров, а именно: о нахождении самого дешевого набора товаров с данным уровнем полезности и о нахождении самого полезного набора товаров с данной стоимостью, если известны цены p, p реализации товара. Как легко можно заключить из рис. для обеих рассматриваемых задач оптимальным является набор товаров, отвечающий точке касания M линии безразличия и прямой p p I, т.е. набор из M, оптимален тогда и только тогда, когда двух товаров p MRS X X M,. (.) p Аналогично, если рассматривается задача об оптимальном производственном плане, т.е. задача о достижении максимально возможного объема производства при данном уровне издержек и о минимизации уровня издержек при данном объеме производства в предположении, что функция издержек линейна C q, q q p q p, где q, q объемы используемых ресурсов X, X, а p, p стоимости единиц этих ресурсов, то производственный план M q, q является оптимальным тогда и только тогда, когда выполнено соотношение (.). При этом MRSX Q q, X M M предельная норма Q замещения первого ресурса вторым, а, производственная функция. q Q q q соответствующая Пример.. Для функции полезности Кобба Дугласа / / U, C, 5, проверьте, будут ли наборы товаров: а) б) 5, 7 самыми дешевыми среди всех наборов, имеющих равные с ними уровни полезности, если стоимости этих товаров составляют p, p.
22 Решение. Согласно вычислениям примера., предельная норма замещения товара X товаром X имеет вид MRSX, X. Тогда 5 p 7 p MRSX, X,5, MRS X, X 5,7. 6 p 5 p Таким образом, набор, 5 является самым дешевым из всех наборов, имеющих с ним равные уровни полезности, а набор 5, 7 является. Задачи для самостоятельного решения 5. Для функции полезности Кобба Дугласа U, / / C, 8, проверьте, будут ли наборы товаров а) б), 5 самыми дешевыми среди всех наборов, имеющих равные с ними уровни полезности, если стоимости этих товаров составляют p 5, p. 6. Для функции полезности U, выяснить, является ли набор товаров (, ) (,5) самым полезным из всех наборов, имеющих равную с ним стоимость, если p 6, p Для производственной функции CES QK, L K L и цен на используемые ресурсы pk и pl 6 выяснить: а) обеспечит ли производственный план K, L 6, наибольший выпуск продукции при данном уровне издержек; б) будет ли при использовании производственного плана K, L,6 минимальным уровень издержек для данного объема выпускаемой продукции?
23 Глава ТРАНСПОРТНАЯ ЗАДАЧА Под транспортной задачей в дальнейшем понимается задача линейного программирования, в которой требуется найти оптимальный (по стоимости) план перевозок некоторого однородного груза от конечного числа поставщиков A, A,, Am с заданными запасами,, m к конечному числу потребителей B, B,, B с потребностями b,, b. Стоимость c перевозки единицы груза от поставщика A к потребителю B предполагается известной. Отметим, что данная постановка задачи может быть значительно расширена или изменена. Например, в приложениях часто рассматриваются задачи перевозки неоднородного груза. Также в качестве критерия оптимальности можно рассматривать время перевозок (транспортная задача по критерию времени). Подобного рода задачи решаются сведением к однородной транспортной задаче, или для них разработаны другие методы, изложение которых остается за рамками данной книги. Постановка задачи Итак, пусть X m матрица, где объем перевозок от -го поставщика к -му потребителю. Тогда общие затраты на перевозку груза определяются функцией zx ( ) m c. Математическая постановка транспортной задачи определяется следующей задачей линейного программирования при условиях m zx ( ) c m
24 m b. m, (.). Первая часть нетривиальных ограничений означает, что все потребности удовлетворены, вторая часть то, что весь груз вывезен от поставщиков. Замечание.. Если запасы и потребности задаются целыми числами, то транспортная задача имеет целочисленное оптимальное решение, поэтому транспортную задачу относят формально к задачам целочисленного линейного программирования. Можно показать, что число базисных переменных в системе ограничений (.) равно m. Поставщики A A B B c c c с Потребители B Определение.. Решение X (оптимальное решение X ) транспортной задачи, удовлетворяющее условиям (.) и имеющее не более m занятой клетки (ненулевой перевозки), будем называть опорным планом (оптимальным опорным планом) транспортной задачи. Исходные данные задачи представляют в виде таблицы.. Общие запасы определяются суммой c с B c c Запасы A c c c c A m cm c m c m c m m m m m m Потребности b b b Таблица. b m, а общая потребность
25 b. Транспортная задача называется задачей с правильным балан- сом, а ее модель закрытой, если m b, то есть суммарные запа- сы поставщиков равны суммарным запросам потребителей. Если m b, то такая задача называется задачей с неправильным ба- лансом, а ее модель открытой. Построение начального опорного плана транспортной задачи Алгоритм решения транспортной задачи с правильным балансом излагается в курсе «Линейная алгебра». В этом параграфе мы напомним основные методы построения начального опорного плана и метод потенциалов решения транспортной задачи. Первым этапом решения является построение начального опорного плана, т.е. плана перевозок, удовлетворяющего всем ограничениям конкретной транспортной задачи. Сущность методов состоит в том, что начальный опорный план находят за не более чем m шагов (по числу базисных переменных), на каждом из которых в транспортной таблице заполняют одну клетку, которую называют занятой. Заполнение одной из клеток обеспечивает полностью либо удовлетворение потребности в грузе одного из пунктов назначения (того, в столбце которого находится заполненная клетка), либо вывоз A A A B B B B b 8 5 Таблица. груза из одного из пунктов отправления (из того, в строке которого находится заполняемая клетка). Различаются эти планы по принципам выбора заполняемых клеток и, в зависимости от этого, могут давать планы, более или менее отличные от оптимального. Пример.. Рассмотрим транспортную задачу, заданную таблицей.. В правом нижнем углу стоит сумма запасов (и, одновременно, сумма потребностей, так как модель закрытая) +6+= =. 5
26 A A A Напомним сначала метод северо-западного угла. Заполнение таблицы начинаем с левого B B B B верхнего (северо-западного) угла таблицы. Так как потребности первого потреби теля В равны 8, а запасы 5 6 первого поставщика A равны, то в клетку AB вписываем максимально Таблица. возможную перевозку 8. В полностью удовлетворены, поэтому первый столбец b 8 5 Потребности исключаем из рассмотрения, а оставшиеся запасы первого поставщика, т.е. 6, переносим следующим потребителям. Мы можем записать потребителю В (столбец В исключается), а оставшиеся В и исключить первую строку из дальнейшего рассмотрения. Далее, так как потребности В равны 5, а единиц груза ему уже доставлены, то оставшиеся единиц доставляются от второго поставщика A (заполняем клетку A B ). Столбец В исключаем из рассмотрения, а оставшиеся запасы второго поставщика ( единиц) записываем потребителю В. Окончательно потребности последнего удовлетворяются за счет поставщика A : вписываем в клетку AB перевозку. Заметим, что, так как исходная задача — с правильным балансом, то потребности последнего потребителя B равны запасам поставщика A, т.е.. Получаем таблицу. с начальным опорным планом 8 X. Суммарная стоимость перевозок равна zx ( ) Из решения видно, что метод северо-западного угла, с одной стороны, достаточно прост с точки зрения построения, а с другой стороны, не учитывает стоимость перевозок. Поэтому опорный план, построенный методом северо-западного угла, как правило, далек от оптимального. 6
27 Построим теперь для этой же задачи начальный опорный план методом минимального тарифа. Суть этого метода состоит в том, что в клетки с наименьшими тарифами помещают максимально возможные перевозки. Итак, в таблице исходной задачи выбираем клетку с минимальным тарифом, т.е. клетку AB с тарифом. Запасы поставщика A равны, а потребности В 8, поэтому в клетку AB вписываем максимально возможную перевозку 8, и потребителя В исключаем из рассмотрения. В оставшейся части таблицы выбираем B минимальный тариф, т.е. B B B клетку AB с тарифом. Запасы поставщика A A 8 6 равны 8 A, а потребности В -, поэтому в клетку AB записываем перевозку и по- A 9 b 8 5 требителя В исключаем из Таблица. рассмотрения. У оставшихся потребителей В, В выбираем клетку с минимальным тарифом. Это AB с тарифом. Запасы (оставшиеся) поставщика A равны 6, а потребности В 5, поэтому в клетку AB записываем максимально возможную перевозку 6 и исключаем поставщика A из дальнейшего рассмотрения. Далее, аналогично в клетку AB записываем и исключаем второго поставщика. В оставшиеся две клетки AB и AB последовательно вписываем перевозку в AB и 9 в AB. Получаем таблицу. с начальным 8 6 опорным планом X. Суммарная стоимость перевозок равна 9 zx ( ) Таким образом, опорный план, построенный методом минимального тарифа, лучше, чем план, полученный методом северо-западного угла. Применим, наконец, к исходной задаче метод аппроксимации Фогеля. Для этого найдем разность между двумя минимальными тарифами для каждой строки и столбца таблицы и запишем их в дополнительно образованные строки и столбцы (см. таблицу.5). В строке A минимальный тариф равен, а следующий за ним, поэтому разность между ними -=; в строке A минимальный тариф равен, а следующий за ним, поэтому разность между равна ; аналогично, 7
28 для строки A разность между минимальным тарифом и следующим за ним 5 равна. Итак, три двойки записываем в первый дополнительный столбец. Аналогично для столбцов разности -=, 5-=, 8-=5 и 6-= записываем в первую дополнительную строку. Теперь из всех разностей выбираем максимальную, т.е. 5 в столбце B, и в клетку AB с минимальным тарифом в этом столбце записываем максимально возможную перевозку. При этом поставщика A исключаем из рассмотрения. Теперь аналогично вычисляем разности между оставшимися минимальными тарифами и заполняем вторые дополнительные столбец и строку, не учитывая тарифы в строке A. Видим, что теперь максимальная разность получается в столбце B и перевозку 8 записываем в клетку AB с минимальным тарифом в этом столбце (первую строку мы исключили из рассмотрения). Столбец B аналогично исключаем из рассмотрения. Как видно из таблицы, на следующем B A A A 8 B B B b 8 5 Разности по столбцам Таблица.5 шаге вписываем перевозку в клетку AB и исключаем столбец B, затем максимально возможную перевозку в клетку AB и исключаем из рассмотрения столбец B. Теперь для вычисления дальнейших разностей остается единственный столбец B, поэтому в качестве разностей по строкам записываем нули. Далее, в клетку AB записываем, а на последнем шаге записываем перевозку в клетку AB. По- Разности по строкам 6 8
29 лучаем таблицу с начальным опорным планом X, а общая стоимость перевозок 8 zx ( ) Отметим, что методом Фогеля обычно получается план, близкий к оптимальному, или сам оптимальный план. Замечание.. В общем случае опорный план транспортной задачи состоит из m занятой клетки (по числу базисных переменных). Такой план называется невырожденным. Нередко при решении транспортной задачи возникает вырожденный план с меньшим числом занятых клеток (когда какие-то из базисных переменных равны ). В этом случае выбирается свободная клетка (или несколько свободных клеток в зависимости от вырожденности плана) с наименьшим тарифом, которая в дальнейшем формально считается занятой с нулевой перевозкой. Решение транспортной задачи методом потенциалов Вторым этапом решения транспортной задачи является проверка построенного плана на оптимальность и его улучшение (если он не оптимален) с помощью метода потенциалов. Применение метода потенциалов основано на следующей теореме Теорема.. Если опорный план X транспортной задачи является оптимальным, то существуют потенциалы поставщиков u. m и потребителей v. удовлетворяющие условиям: u v c при (для занятых клеток), (.) u v c при (для свободных клеток). (.) Условия (.) образуют систему с m+ неизвестными u, v и, в общем случае, m уравнений. Так как число неизвестных системы на единицу больше числа уравнений, то одну из неизвестных можно задать произвольно, а остальные найти из системы. 9
30 Числа u v c называют оценками свободных клеток. Таким образом, согласно теореме, опорный план будет оптимален, если u -5 v для всех свободных клеток таблицы оценки неположительные. Проверим теперь оптимальность планов, построенных выше. Пример.. Сначала рассмотрим начальный опорный план, построенный методом Таблица.6 минимального тарифа и методом Фогеля. Потенциалы будем записывать в первые строку и столбец вместо обозначений поставщиков и потребителей. Так как одну из неизвестных можно задать произвольно, то u удобнее всего выбирать в качестве исходной переменной тот потенциал, в строке которого больше всего занятых клеток. Здесь, таким образом, полагаем 9 9 u. Из условий (.) b u v, u v 8, 8 5 Таблица.7 u v сразу находим, что v, v 8, v. Далее, из u v 5 получаем, что u, из uv следует u 5, а из u v заключаем, что v. Все потенциалы найдены (см. таблицу.6). Теперь находим оценки для свободных клеток u v c, u v c, u v c 6, u v c, u v c 5, u v c. Результат записываем в таблицу.6 (где в свободных клетках в квадратике записаны оценки). Все оценки отрицательны, поэтому план X оптимален и zm z( X ) b 8 5 v
31 Пример.. Теперь проверим на оптимальность план перевозок, полученный методом минимального тарифа. Ясно, что в силу большей суммарной стоимости перевозок план не оптимален, но вычисление потенциалов и оценок необходимо для того, чтобы этот начальный опорный план улучшить. Проделав вычисления, ана- ( ) () + 9 логичные примеру., для опорного плана примера., построенно- Рис.. (8) () го методом минимального тарифа, получаем таблицу.7. Как видим, среди оценок есть положительные, поэтому, как и ожидалось, опорный план X 8 6 не оптимален. 9 Чтобы улучшить опорное решение X транспортной задачи, введем понятие цикла. Напомним, что циклом называется последовательность клеток таблицы транспортной задачи, в которой две и только две соседние клетки расположены в одной строке или столбце. Цикл обычно изображают в виде замкнутой ломаной линии, соединяющей вершины цикла, расположенные в клетках таблицы. u — v Для построения нового опорного плана в таблице выбираем свободную клетку с максимальной положительной оценкой (клетка AB ) и формируем цикл, одной из вершин которого является выбранная клетка, а остальные клетки занятые. Легко видеть, что это цикл, соединяющий клетки AB, AB, AB, и AB. Кроме этого, сопоставим каждой вершине цикла знак и перевозку, при этом свободной клетке сопоставляем знак, а для остальных клеток знаки чередуются. Получим следующий цикл, изображенный на рисунке.. Теперь сделаем перестановку по циклу, а именно: из всех вершин, отмеченных минусом, вычтем минимум из всех перевозок, означенных этим знаком, т.е. в читаем m(8,9) 8, а ко всем вершинам с прибавим. Получим новые значения перевозок, обозначенные на рис.. в скобках b 8 5 Таблица.8
32 При этом клетка AB (обозначена знаком «()») становится свободной, и мы получаем новый опорный план (таблица.8). Общая стоимость перевозок равна zx ( ) Полученный план лучше начального, и, оценивая его оптимальность с помощью метода потенциалов, видим, что есть положительные оценки, и план не оптимален (см. таблицу.8). Снова выбираем свободную клетку с положительной оценкой (здесь такая клетка + единственная клетка AB ) и формируем цикл с вершиной в этой клетке. () Рис.. ( ) Таковым является цикл, соединяющий клетки AB, AB, AB и AB (рис..). Так как m(,), то после перестановки по циклу получаем новый план X, фактически уже возникавший 8 в таблице.6. Его оптимальность уже была проверена. Задачи для самостоятельного решения Решить методом потенциалов транспортные задачи B B B B B B B B A A A A A A 5 8 b b 6 B B B B B B B B A 8 9 A A 5 6. A A 6 A b b 7 B B B B B B B B A A. A A A 8 A b 9 5 b 5 7 () + ()
33 . A A A b B B B B A A A b B B B B Открытая модель транспортной задачи Напомним, что транспортная задача m называется задачей с неправильным балансом, а ее модель открытой, если m b, т.е. суммарные запасы не равны суммарным потребностям. Открытую задачу можно свести к замкнутой:. Если A A A B B B B b 8 5 Таблица.9 m b, то вводят фиктивного потребителя 5 6 u B B B B B 5 v Разности по строкам 7 7 b B с по- Разности по столбцам Таблица.
34 требностью b b и m нулевыми тарифами перевозок в столбце.. Если m b, то вво- дят фиктивного поставщика A A A A B B B B m m b 6 6 с запасом m b и нулевыми тарифами перевозок в строке. Пример.. Рассмотрим задачу примера., но с измененным запасами, заданную таблицей.9. Так как сумма запасов 5 6 больше суммы (6) 6 потребностей + ( ) , то вводим 6 фиктивного потребителя B 5 с нулевыми тарифами перевозок и по- + () () + () 8 требностями (таблица.). () Рис.. Методом аппроксимации Фогеля построим начальный план и методом потенциалов проверим полученный план на оптимальность. u v b 6 6 Таблица. Получаем, что все оценки отрицательны, поэтому полученный план 9 X и Таблица. (для его записи мы отбрасываем столбец фиктивного потребителя B 5) оптимален F X 58. Как следствие неправильного баланса имеем, что от поставщика A не вывезено единиц груза. Пример.5. В транспортной задаче, заданной таблицей., сумма запасов равна, а потребностей 5. Поэтому необходимо ввести дополнительного поставщика A с запасом и тарифами перевозок (см. таблицу.)
35 Построим начальный план методом минимального тарифа и вычислим потенциалы. Легко видеть, что план не оптимален, максимальная положительная оценка равна 5, и вершинами цикла являются клетки AB, AB, AB, AB, AB и AB. Получается цикл «с самопересечением», изображенный на рис. Получаем, что m6,8 6. Заметим, что после перестановки по циклу сразу в u двух клетках получается v 8 нулевая перевозка. 8 6 Замечание Если после перестановки 7 по циклу больше чем в одной клетке образуется ну левая перевозка, то одна из них становится свободной (желательно, с максимальным тарифом), а осталь b 6 6 ные считаются занятыми с Таблица. нулевой перевозкой, чтобы число занятых клеток оставалось равным m. Таким образом, получаем новый план, указанный в таблице.. Имеется единственная клетка AB с положительной оценкой, причем в цикле, изображенном на рисунке., одна из клеток, означенных минусом, имеет нулевую перевозку. Замечание.. Если занятая клетка с нулевой перевозкой попала в цикл и соответствует знаку (при этом ), то перестановка u по циклу сводится к тому, что свободная клетка v объявляется занятой с 7 нулевой перевозкой, а занятая клетка с нулевой b 6 6 Таблица. 8 ( ) () + Рис.. перевозкой становится свободной. Таким образом, занятая нулевая и свободная клетки меняются местами (рис..). Проверяя план на оптималь- + () () 5
36 ность (таблица.), убеждаемся, что все оценки отрицательны, 6 X (мы отбрасываем строку фиктивного поставщика) оптимален, и F X. В результате получаем, что потреб- ности потребителя B удовлетворены не полностью. Задачи для самостоятельного решения Решить транспортные задачи методом потенциалов B B B B B B B B A 7 7 A 6 6. A 7 7. A A A b b 5 5 B B B B B B B B A A A A A A 8 b b 85 5 B B B B B B B B A 7 7 A. A A A 9 A b b Определение оптимального плана транспортных задач с дополнительными ограничениями При решении транспортных задач методом потенциалов возможно учитывать дополнительные ограничения на перевозки. Ниже перечислены варианты различных постановок транспортных задач и 6
37 даны соответствующие методы сведения к закрытой транспортной задаче.. Если в закрытой транспортной задаче перевозки от поставщика A к потребителю B не могут быть осуществлены (блокировка), то для определения оптимального решения задач предполагают, что тариф перевозки единицы груза от A к B равен сколь угодно большому числу M.. Если дополнительным условием в транспортной задаче является обеспечение перевозки от поставщика A к потребителю B в точности единиц груза, то в клетку AB записывают указанное число, а эту клетку считают свободной со сколь угодно большим тарифом M.. Если от поставщика A к потребителю B должно быть пере- A и потребности везено не менее единиц груза, что запасы пункта пункта B полагают меньше фактических на единиц. После нахождения оптимального плана перевозку, стоящую в клетке AВ, увеличивают на единиц.. Если от поставщика A к потребителю не более B требуется перевезти единиц груза, то u v 8 вводят дополнительного потребителя B -5 B, которому записывают те же тарифы, что и для 8 6 B, за исключением тарифа в ой строке, который считают b равным сколь угодно большому 8 5 числу M. Потребности пункта Таблица.5 B считают равными, а потребности B полагают равными b. Пример.6. Найти решение транспортной задачи, заданной таблицей.5, если из A в B и из A в B перевозки не могут быть осуществлены, из A в B должно быть завезено не менее ед. груза, а из A в B ровно 7 ед. 7
38 u Решение. Так v 7 M -5 как из A в B и из A в 8 M 8 B перевозки не могут M быть осуществлены, то M M в клетках AB и AB M 5 6 тарифы считаем равными некоторому боль- M M 6 b 8 5 шому числу M. В Таблица.6 клетке AB перевозку считаем равной 7, а тариф равным M, и эту клетку в дальнейшем полагаем свободной. Кроме этого, запасы A и потребности B уменьшаем на. Получаем таблицу.6, строим начальный опорный план методом 8 минимального тарифа, находим потенциалы и оценки свободных кле- + () () ток (см. таблицу.6). Имеем единственную положительную оценку (8) + 8 M и строим цикл, соединяющий клетки AB, AB, AB ( ) Рис..5 и AB (рис..5). В клетках, означенных минусом, перевозки одинаковы, поэтому в соответствии с u v -7-5 замечанием., клетку AB считаем занятой с нулевой перевозкой, а AB свободной. После перестановки по циклу получаем новый план (таблица.7). Так как все оценки отрицательны, то данная таблица заключительная. Увеличиваем перевозку в клетке AB на, получим оптимальный план перевозок, удовлетворяющий всем ограничениям задачи: X 8 7 и 6 F X M M 8 5 M M b 8 5 Таблица.7 8
39 u Пример.7. v — — Найти решение 5 6 транспортной задачи, 8 M заданной таблицей M.5, если из A в B 7 5 M 6 7 перевозки запрещены, а из A M M 9 M 9 M M 9 в B b должно быть завезено не более 5 ед Таблица.8 груза, а из A в B не менее ед. груза. Решение. Так как из A в B перевозки запрещены, то тариф в AB считаем рав- ( ) 5 + ным M. Запасы A и потребности B + (5) уменьшаем на, (5) Рис..6 а также вводим дополнительного потребителя B 5 с потребностями 8 5. Соответственно, в клетке AB 5 стоимость перевозок считаем равной M, а потребности B приравниваем к 5. Получаем таблицу.8. Найдем начальное опорное решение методом минимального тарифа, потенциалы и оценки. Анализируя циклы, проходящие через клетки с максимальной положительной оценкой M 9, u v 5 M 8 6 вибираем цикл, содержащий клетку -5 9 M 7 6 AB, так как при 8 M этом перевозка в M M 7 5 M ячейке AB максимально уменьшается. 6 7 М-8 5 M 9 5 M M 9 Итак, в результате b перестановки по Таблица.9 циклу, соединяющему клетки AB, AB, AB и AB (см. рис..6), получаем новую таблицу.9. Опять получаем две ячейки с максимальной положительной оценкой ( ) + M 9. Так как для цикла с началом в AB + 5 перевозка в клетке AB () () Рис..7 уменьшается на, а для цикла с началом 9
источник
- http://studopedia.ru/17_109891_zadacha-.html
- http://lektsii.org/16-32196.html
- http://docplayer.ru/26481178-Metody-optimalnyh-resheniy.html